Question

【題目】將函數(shù)y＝sin2x－cos2x的圖象向左平移m（m＞0）個單位以后得到的圖象與函數(shù)y＝ksinxcosx（k＞0）的圖象關于（，0）對稱，則k＋m的最小正值是

A. 2＋ B. 2＋ C. 2＋ D. 2＋

Answer 1

【答案】C

【解析】

由題意可得y=﹣cos（2x﹣2m）的圖象和y=sin2x（k＞0）的圖象關于點對稱，設點

P（x0，y0）為y=﹣cos（2x﹣2m）上任意一點，則該點關于對稱點為在

y=sin2x（k＞0）的圖象上，故有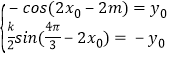，求得k=2，且cos（2x0﹣）=cos

（2x0﹣2m），由此求得k+m的最小正值．

將函數(shù)y=sin2x﹣cos2x=﹣cos2x的函數(shù)圖象向右平移m個單位以后得到y=﹣cos2（x﹣m）=

﹣cos（2x﹣2m）的圖象，

根據(jù)所得圖象與y=ksinxcosx=sin2x（k＞0）的圖象關于對稱，

設點P（x0，y0）為y=﹣cos（2x﹣2m）上任意一點，

則該點關于對稱點為在y=sin2x（k＞0）的圖象上，故有

，

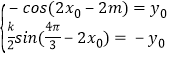所以k=2，sin（2x0﹣）=cos（2x0﹣2m），即cos（2x0﹣）=cos（2x0﹣2m），

∴﹣2m=﹣+2kπ，k∈Z，即 2m=﹣2kπ，k∈Z，故m的最小正值為，

則k+m的最小正值為2+．故答案為：C