
【題目】如圖, ![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.
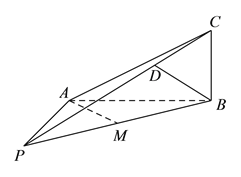
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(![]() )見解析(
)見解析(![]() )
)![]() (
(![]() )見解析.
)見解析.
【解析】試題分析:(1)![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ;(2)建立空間直角坐標系,求得平面
;(2)建立空間直角坐標系,求得平面![]() 和平面
和平面![]() 的法向量,求得二面角的余弦值;(3)由點
的法向量,求得二面角的余弦值;(3)由點![]() 在線段
在線段![]() 上,則
上,則![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,所以存在點
,所以存在點![]() 。
。
試題解析:
(![]() )證明:∵
)證明:∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() 為
為![]() 的中點,
的中點,
∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
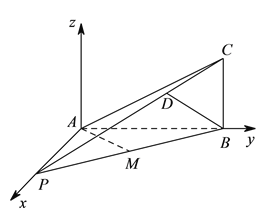
(![]() )如圖,在平面
)如圖,在平面![]() 內作
內作![]() ,則
,則![]() ,
, ![]() ,
, ![]() 兩兩垂直,建立空間直角坐標系
兩兩垂直,建立空間直角坐標系![]() .則
.則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則:
,則:
![]() ,即
,即![]() ,令
,令![]() ,則
,則![]() .
.
∴![]() .
.
由(![]() )可知
)可知![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
∴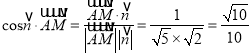 .
.
∵二面角![]() 為銳角,
為銳角,
∴二面角![]() 的余弦值為
的余弦值為![]() .
.
(![]() )證明:設
)證明:設![]() 是線段
是線段![]() 上一點,且
上一點,且![]() ,
, ![]() ,
,
即![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.
由![]() ,得
,得![]() ,
,
∴線段![]() 上存在點
上存在點![]() ,使得
,使得![]() ,此時
,此時![]() .
.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】某項競賽分為初賽、復賽、決賽三個階段進行,每個階段選手要回答一個問題.規定正確回答問題者進入下一階段競賽,否則即遭淘汰.已知某選手通過初賽、復賽、決賽的概率分別是![]()
![]() ,且各階段通過與否相互獨立.
,且各階段通過與否相互獨立.
(1)求該選手在復賽階段被淘汰的概率;
(2)設該選手在競賽中回答問題的個數為![]() ,求
,求![]() 的分布列、數學期望.
的分布列、數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .點
.點![]() 在棱
在棱![]() 上,平面
上,平面![]() 與棱
與棱![]() 相交于點
相交于點![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求證: ![]() 平面
平面![]() .
.
(Ⅲ)求三棱錐![]() 的體積的取值范圍.
的體積的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數集![]() ,其中
,其中![]() ,
, ![]() ,定義向量集
,定義向量集![]() .若對于任意
.若對于任意![]() ,使得
,使得![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .例如
.例如![]() 具有性質
具有性質![]() .
.
(![]() )若
)若![]() ,且
,且![]() 具有性質
具有性質![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 具有性質
具有性質![]() ,求證:
,求證: ![]() ,且當
,且當![]() 時,
時, ![]() .
.
(![]() )若
)若![]() 具有性質
具有性質![]() ,且
,且![]() ,
, ![]() (
(![]() 為常數),求有窮數列
為常數),求有窮數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,設點
中,設點![]() 是橢圓
是橢圓![]() :
: ![]() 上一點,從原點
上一點,從原點![]() 向圓
向圓![]() :
: ![]() 作兩條切線分別與橢圓
作兩條切線分別與橢圓![]() 交于點
交于點![]() ,
, ![]() ,直線
,直線![]() ,
, ![]() 的斜率分別記為
的斜率分別記為![]() ,
, ![]() .
.

(1)求證: ![]() 為定值;
為定值;
(2)求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() 的方程為
的方程為![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,曲線
軸的正半軸,建立平面直角坐標系,曲線![]() 的參數方程為
的參數方程為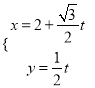 ,(
,( ![]() 為參數)
為參數)
(1)求曲線![]() 的參數方程和曲線
的參數方程和曲線![]() 的普通方程;
的普通方程;
(2)求曲線![]() 上的點到曲線
上的點到曲線![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的首項![]() ,
, ![]() ,
, ![]() .
.
(1)求證:數列 為等比數列;
為等比數列;
(2)記![]() ,若Sn<100,求最大正整數n;
,若Sn<100,求最大正整數n;
(3)是否存在互不相等的正整數m,s,n,使m,s,n成等差數列,且am-1,as-1,an-1成等比數列?如果存在,請給以證明;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉徽(約公元 225 年—295 年)是魏晉時期偉大的數學家,中國古典數學理論的奠基人之一,他的杰作《九章算術注》和《海島算經》是中國寶貴的古代數學遺產. 《九章算術·商功》中有這樣一段話:“斜解立方,得兩壍堵. 斜解壍堵,其一為陽馬,一為鱉臑.” 劉徽注:“此術臑者,背節也,或曰半陽馬,其形有似鱉肘,故以名云.” 其實這里所謂的“鱉臑(biē nào)”,就是在對長方體進行分割時所產生的四個面都為直角三角形的三棱錐. 如圖,在三棱錐![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,則三棱錐
,則三棱錐![]() 的外接球的球面面積為__________.
的外接球的球面面積為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com