
【題目】若數列![]() 滿足
滿足![]() ,數列
,數列![]() 為
為![]() 數列,記
數列,記![]() .
.
(1)寫出一個滿足![]() ,且
,且![]() 的
的![]() 數列
數列![]() ;
;
(2)若![]() ,
,![]() ,證明:
,證明:![]() 數列
數列![]() 是遞增數列的充要條件是
是遞增數列的充要條件是![]() ;
;
(3)對任意給定的整數![]() ,是否存在首項為0的
,是否存在首項為0的![]() 數列
數列![]() ,使得
,使得![]() ?如果存在,寫出一個滿足條件的
?如果存在,寫出一個滿足條件的![]() 數列
數列![]() ;如果不存在,說明理由.
;如果不存在,說明理由.
【答案】(1)0,1,0,1,0;(2)證明見解析;(3)見解析
【解析】
(1)根據![]() 與
與![]() 和
和![]() 可考慮寫出
可考慮寫出![]() 交替的數列.
交替的數列.
(2)先證明必要性,根據![]() 數列
數列![]() 是遞增數列,可得
是遞增數列,可得![]() ,進而求得
,進而求得![]() .再證明充分性,因為
.再證明充分性,因為![]() ,故
,故![]() ,再累加可得
,再累加可得![]() 證明即可.
證明即可.
(3) 設![]() ,則
,則![]() ,再累加求得
,再累加求得![]() ,再分析
,再分析![]() 的奇偶,根據整除的性質,先假設存在再證明矛盾即可.
的奇偶,根據整除的性質,先假設存在再證明矛盾即可.
(1)0,1,0,1,0是一個滿足條件的![]() 數列
數列![]() .
.
(2)必要性:因為![]() 數列
數列![]() 是遞增數列,
是遞增數列,
所以![]() ,
,
所以![]() 是首項為13,公差為1的等差數列.
是首項為13,公差為1的等差數列.
所以![]() ,
,
充分性:由于![]() ,故
,故![]() ,
,
![]() ,
,
……
![]() ,
,
所以![]() ,即
,即![]() ,
,
又因為![]() ,
,![]() ,
,
所以![]() ,
,
故![]() ,即
,即![]() 是遞增數列.
是遞增數列.
綜上所述,結論成立.
(3)設![]() ,則
,則![]() ,
,
因為![]() ,
,
![]() ,
,
……
![]() ,
,
所以![]()
![]()
![]() ,
,
因為![]() ,所以
,所以![]() 為偶數(
為偶數(![]() )
)
所以![]() 為偶數,
為偶數,
所以要使![]() ,必須使
,必須使![]() 為偶數,
為偶數,
即4整除![]() ,亦即
,亦即![]() 或
或![]() ,
,
當![]() 時,
時,![]() 數列
數列![]() 的項滿足
的項滿足![]() ,
,![]() ,
,![]() ,
,
此時,有![]() 且
且![]() 成立,
成立,
當![]() 時,
時,![]() 數列
數列![]() 的項滿足
的項滿足![]() ,
,![]() ,
,![]() ,
,![]() 時,亦有
時,亦有![]() 且
且![]() 成立,
成立,
當![]() 或
或![]() 時,
時,![]() 不能被4整除,此時不存在數列
不能被4整除,此時不存在數列![]() ,使得
,使得![]() 且
且![]() 成立.
成立.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax﹣(a+2)lnx![]() 2,其中a∈R.
2,其中a∈R.
(1)當a=4時,求函數f(x)的極值;
(2)試討論函數f(x)在(1,e)上的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省確定從2021年開始,高考采用“![]() ”的模式,取消文理分科,即“3”包括語文、數學、外語,為必考科目;“1”表示從物理、歷史中任選一門;“2”則是從生物、化學、地理、政治中選擇兩門,共計六門考試科目.某高中從高一年級2000名學生(其中女生900人)中,采用分層抽樣的方法抽取
”的模式,取消文理分科,即“3”包括語文、數學、外語,為必考科目;“1”表示從物理、歷史中任選一門;“2”則是從生物、化學、地理、政治中選擇兩門,共計六門考試科目.某高中從高一年級2000名學生(其中女生900人)中,采用分層抽樣的方法抽取![]() 名學生進行調查.
名學生進行調查.
(1)已知抽取的![]() 名學生中含男生110人,求
名學生中含男生110人,求![]() 的值及抽取到的女生人數;
的值及抽取到的女生人數;
(2)學校計劃在高二上學期開設選修中的“物理”和“歷史”兩個科目,為了了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生進行問卷調杳(假定每名學生在這兩個科目中必須洗擇一個科目且只能選擇一個科目).下表是根據調查結果得到的
名學生進行問卷調杳(假定每名學生在這兩個科目中必須洗擇一個科目且只能選擇一個科目).下表是根據調查結果得到的![]() 列聯表,請將列聯表補充完整,并判斷是否有
列聯表,請將列聯表補充完整,并判斷是否有![]() 的把握認為選擇科目與性別有關?說明你的理由;
的把握認為選擇科目與性別有關?說明你的理由;
性別 | 選擇物理 | 選擇歷史 | 總計 |
男生 | 50 | ||
女生 | 30 | ||
總計 |
(3)在(2)的條件下,從抽取的選擇“物理”的學生中按分層抽樣抽取6人,再從這6名學生中抽取2人,對“物理”的選課意向作深入了解,求2人中至少有1名女生的概率.
附: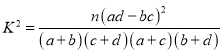 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面積等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com