
【題目】已知函數![]()
(1)當![]() 時,求滿足方程
時,求滿足方程![]() 的
的![]() 的值;
的值;
(2)若函數![]() 是定義在R上的奇函數.
是定義在R上的奇函數.
①若存在![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
②已知函數![]() 滿足
滿足![]() ,若對任意
,若對任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值
的最大值
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)解方程![]() 求出
求出![]() 的值即可;
的值即可;
(2)根據函數![]() 是定義在R上的奇函數,由定義列出方程,求出
是定義在R上的奇函數,由定義列出方程,求出![]() ,
,![]()
對于①,利用函數單調性的定義證明![]() 的單調性,利用單調性化簡不等式得到
的單調性,利用單調性化簡不等式得到![]() ,由
,由![]() ,即可得到實數
,即可得到實數![]() 的取值范圍;
的取值范圍;
對于②,由![]() 的解析式得到
的解析式得到![]() 的解析式,化簡
的解析式,化簡![]() ,結合換元法以及基本不等式得到實數
,結合換元法以及基本不等式得到實數![]() 的最大值.11
的最大值.11
解:(1)因為![]() ,
,![]() ,所以
,所以![]() ,
,
化簡得![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
所以![]() .
.
(2)因為![]() 是奇函數,
是奇函數,
所以![]() ,所以
,所以![]()
化簡變形得:![]()
要使上式對任意![]() 恒成立,則
恒成立,則![]() 且
且![]()
解得:![]() 或
或![]() ,因為
,因為![]() 的定義域是
的定義域是![]() ,所以
,所以![]() 舍去
舍去
所以![]() ,
,![]() ,所以
,所以![]() .
.
①![]() ,
,
對任意![]() ,
,![]() ,且
,且![]() 有:
有: ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因此![]() 在
在![]() 上單調遞增,
上單調遞增,
因為![]() ,當
,當![]() 時成立,所以
時成立,所以![]() ,當
,當![]() 時成立,
時成立,
即![]() ,當
,當![]() 時成立,
時成立,
當![]() 時,
時,![]() ,所以
,所以![]() .
.
②因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,
不等式![]() 恒成立,即
恒成立,即![]() ,
,
令![]() ,因為
,因為![]() 且
且![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,當
,當![]() 時恒成立,即
時恒成立,即![]() ,當
,當![]() 時恒成立,
時恒成立,
因為![]() ,
,![]() ,當且僅當
,當且僅當![]() 時,等號成立,
時,等號成立,
所以![]() ,即實數
,即實數![]() 的最大值為
的最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知m,n是兩條不同的直線,α,β,γ是三個不同的平面,則下列說法正確的是( )
A.若m∥α,n∥α,則 m∥n
B.若α⊥γ,β⊥γ,則α∥β
C.若m⊥α,n⊥β,且α⊥β,則m⊥n.
D.若m∥α,n∥α,且mβ, nβ,則α∥β
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(-2,0),B(2,0),過點A作直線l與以A,B為焦點的橢圓交于M,N兩點,線段MN的中點到y軸的距離為![]() ,且直線l與圓x2+y2=1相切,則該橢圓的標準方程是________,過A點的橢圓的最短弦長為________.
,且直線l與圓x2+y2=1相切,則該橢圓的標準方程是________,過A點的橢圓的最短弦長為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義函數![]() ,其中x為自變量,a為常數.
,其中x為自變量,a為常數.
(1)若當x∈[0,2]時,函數fa(x)的最小值為﹣1,求a的值;
(2)設全集U=R,集合A={x|f3(x)≥0},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠![]() 中,求a的取值范圍.
中,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在國慶期間,某商場進行優惠大酬賓活動,在活動期間,商場內所有商品按標價的80%出售;同時,當顧客在該商場內消費滿一定金額(![]() 元)后,還可按如下方案獲得相應金額(
元)后,還可按如下方案獲得相應金額(![]() 元)的獎券:
元)的獎券: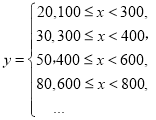 根據上述優惠方案,顧客在該商場購物可以獲得雙重優惠例如,購買標價為300元的商品,則消費金額為240元,獲得的優惠額為:
根據上述優惠方案,顧客在該商場購物可以獲得雙重優惠例如,購買標價為300元的商品,則消費金額為240元,獲得的優惠額為:![]() (元).設購買商品得到的
(元).設購買商品得到的![]() ,試問:
,試問:
(1)購買一件標價為800元的商品,顧客得到的優惠率是多少?
(2)對于標價在![]() (元)內的商品,要使顧客購買某商品獲得30%的優惠率,則該商品的標價是多少?
(元)內的商品,要使顧客購買某商品獲得30%的優惠率,則該商品的標價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第23屆冬季奧運會于2018年2月9日至2月25日在韓國平昌舉行,期間正值我市學校放寒假,寒假結束后,某校工會對全校教職工在冬季奧運會期間每天收看比賽轉播的時間作了一次調查,得到如下頻數分布表:

(1)若講每天收看比賽轉播時間不低于3小時的教職工定義為“體育達人”,否則定義為“非體育達人”,請根據頻數分布表補全![]() 列聯表:
列聯表:

并判斷能否有90%的把握認為該校教職工是否為“體育達人”與“性別”有關;
(2)在全校“體育達人”中按性別分層抽樣抽取6名,再從這6名“體育達人”中選取2名作冬奧會知識講座.記其中女職工的人數為![]() ,求的
,求的![]() 分布列與數學期望.
分布列與數學期望.
附表及公式:
![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以坐標原點
,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的參數方程為
的參數方程為![]() (t為參數).
(t為參數).
(1)寫出曲線![]() 的參數方程和直線
的參數方程和直線![]() 的普通方程;
的普通方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,,求點
上一點,,求點![]() 到直線
到直線![]() 的最小距離.
的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() :
: ![]() 經過伸縮變換
經過伸縮變換![]() 后得到曲線
后得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求出曲線![]() 、
、![]() 的參數方程;
的參數方程;
(Ⅱ)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 、
、![]() 上的動點,求
上的動點,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com