
【題目】已知定義域為![]() 的函數
的函數![]() 是奇函數.
是奇函數.
(1)求![]() 的值;
的值;
(2)證明: ![]() 為
為![]() 上的增函數;
上的增函數;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ; (2)見解析;(3)
; (2)見解析;(3)![]() .
.
【解析】試題分析:(1)根據奇函數的定義,取x=1,得f(1)+f(﹣1)=0,解之得a=2,再經過檢驗可得當a=2時,f(x)+f(﹣x)=0對x∈R恒成立,所以f(x)是奇函數;(2)令t=2x,得![]() ,再用單調性的定義,證出當x1∈R,x2∈R且x1<x2時,y1﹣y2=
,再用單調性的定義,證出當x1∈R,x2∈R且x1<x2時,y1﹣y2=![]() ,討論可得y1<y2,所以f(x)在R上是增函數;(3)因為f(x)是奇函數,并且在R上是增函數,所以原不等式對任意的x∈R恒成立,即mx2+1>mx﹣1對任意的x∈R恒成立,化簡整理得關于m的一元二次不等式,最后經過分類討論,可得實數m的取值范圍為0≤m<8.
,討論可得y1<y2,所以f(x)在R上是增函數;(3)因為f(x)是奇函數,并且在R上是增函數,所以原不等式對任意的x∈R恒成立,即mx2+1>mx﹣1對任意的x∈R恒成立,化簡整理得關于m的一元二次不等式,最后經過分類討論,可得實數m的取值范圍為0≤m<8.
試題解析:
(1)∵函數是奇函數,
∴![]() ,
,
可得 ,解之得:
,解之得: ![]() ,
,
檢驗: ![]() 時,
時, ![]() ,
,
∴
∴![]() 對
對![]() 恒成立,即
恒成立,即![]() 是奇函數.
是奇函數.
∴![]()
(2)證明:令![]() ,則
,則![]()
![]()
![]()
![]()
設![]() ,
, ![]() ,且
,且![]() ,∵
,∵![]() 在
在![]() 上是增函數,∴
上是增函數,∴![]() ,
,
當![]() 時,∴
時,∴ ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,可得
,可得![]() 在
在![]() 上是增函數.
上是增函數.
(3)∵![]() 是奇函數,
是奇函數,
∴不等式![]() 等價于
等價于![]()
∵![]() 在
在![]() 上是增函數,
上是增函數,
∴對任意的![]() ,原不等式恒成立,即
,原不等式恒成立,即![]() 對任意
對任意![]() 恒成立,
恒成立,
化簡整理得: ![]() 對任意
對任意![]() 恒成立,
恒成立,
(1)當![]() 時,不等式即為
時,不等式即為![]() 恒成立,符合題意;
恒成立,符合題意;
(2)當![]() 時,有
時,有![]() ,即
,即![]() ,
,
綜上所述:可得實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】設命題![]() 是
是![]() 的必要而不充分條件;
的必要而不充分條件;
設命題![]() 實數
實數![]() 滿足方程
滿足方程![]() 表示雙曲線.
表示雙曲線.
(1)若“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了監控某種零件的一條生產線的生產過程,檢驗員每天從該生產線上隨機抽取16個零件,并測量其尺寸(單位:cm).根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件的尺寸服從正態分布![]() .
.
(1)假設生產狀態正常,記X表示一天內抽取的16個零件中其尺寸在![]()
之外的零件數,求![]() ;
;
(2)一天內抽檢零件中,如果出現了尺寸在![]() 之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
下面是檢驗員在一天內抽取的16個零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得![]() ,
, 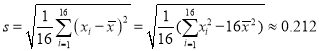 ,其中
,其中![]() 為抽取的第
為抽取的第![]() 個零件的尺寸,
個零件的尺寸, ![]() .
.
用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() ,利用估計值判斷是否需對當天的生產過程進行檢查?剔除
,利用估計值判斷是否需對當天的生產過程進行檢查?剔除![]() 之外的數據,用剩下的數據估計
之外的數據,用剩下的數據估計![]() 和
和![]() (精確到0.01).
(精確到0.01).
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直角梯形![]() 中,
中,![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,![]() .沿
.沿![]() 將
將![]() 折起,使
折起,使![]() 至
至![]() 處,且
處,且![]() ;然后再將
;然后再將![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 處,且面
處,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同側.
的同側.

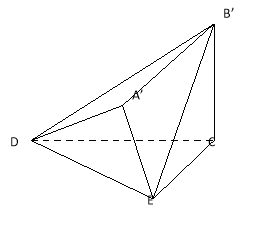
(Ⅰ) 求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 與平面
與平面![]() 所構成的銳二面角的余弦值.
所構成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用定義證明函數![]() 在
在![]() 上是增函數;
上是增函數;
(2)探究是否存在實數![]() ,使得函數
,使得函數![]() 為奇函數?若存在,求出
為奇函數?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)在(2)的條件下,解不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出![]() 該產品獲利潤500元,未售出的產品,每
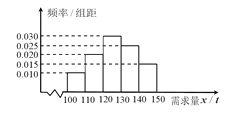
該產品獲利潤500元,未售出的產品,每![]() 虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了
虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該農產品.以
該農產品.以![]() (
(![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量, ![]() (單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(Ⅰ)將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)根據直方圖估計利潤![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】語文成績服從正態分布![]() ,數學成績的頻率分布直方圖如下:
,數學成績的頻率分布直方圖如下:
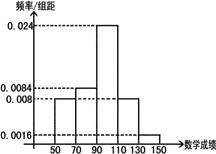
(Ⅰ)如果成績大于135的為特別優秀,這500名學生中本次考試語文、數學特別優秀的大約各多少人?(假設數學成績在頻率分布直方圖中各段是均勻分布的)
(Ⅱ)如果語文和數學兩科都特別優秀的共有6人,從(Ⅰ)中的這些同學中隨機抽取3人,設三人中兩科都特別優秀的有![]() 人,求
人,求![]() 的分布列和數學期望.
的分布列和數學期望.
(附參考公式)若![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為橢圓
為橢圓![]() 的左焦點,且兩焦點與短軸的一個頂點構成一個等邊三角形,直線
的左焦點,且兩焦點與短軸的一個頂點構成一個等邊三角形,直線![]() 與橢圓
與橢圓![]() 有且僅有一個交點
有且僅有一個交點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與
與![]() 軸交于
軸交于![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于兩不同點
交于兩不同點![]() ,
, ![]() ,若
,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com