
【題目】已知函數(shù)![]() ,點(diǎn)
,點(diǎn)![]() 分別在
分別在![]() 的圖象上.
的圖象上.
(1)若函數(shù)![]() 在
在![]() 處的切線恰好與
處的切線恰好與![]() 相切,求
相切,求![]() 的值;
的值;
(2)若點(diǎn)![]() 的橫坐標(biāo)均為
的橫坐標(biāo)均為![]() ,記
,記![]() ,當(dāng)
,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 取得極大值,求
取得極大值,求![]() 的范圍.
的范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)利用導(dǎo)數(shù)求解出函數(shù)![]() 在
在![]() 處的切線方程,聯(lián)立方程組,利用判別式,即可求解
處的切線方程,聯(lián)立方程組,利用判別式,即可求解![]() 的值;(2)由
的值;(2)由![]() ,得出函數(shù)的解析式
,得出函數(shù)的解析式![]() ,利用導(dǎo)數(shù)等于零,
,利用導(dǎo)數(shù)等于零,
![]() ,設(shè)
,設(shè)![]() ,再由存在唯一的
,再由存在唯一的![]() ,使得
,使得![]() ,在分三種情況分類討論,即可求解
,在分三種情況分類討論,即可求解![]() 的范圍.
的范圍.
試題解析:(1)由![]() ,∴在
,∴在![]() 即切點(diǎn)為
即切點(diǎn)為![]() 處的切線斜率
處的切線斜率![]() ,
,
即切線為![]() ,
,
∴聯(lián)立![]() ,得
,得![]() ,
,
由相切得![]() ,
,
解得![]()
(2)![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() 取得極值,則
取得極值,則![]() 或
或![]() ,
,
∴![]() ,令
,令![]() ,該函數(shù)在
,該函數(shù)在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∴存在唯一的![]() ,使得
,使得![]() ,
,
①若![]() ,則
,則
|
| 0 |
|
|
|
| - | 0 | + | 0 | - |
| 遞減 | 極小 | 遞增 | 極大 | 遞減 |
此時(shí)![]() 時(shí)為極小值;
時(shí)為極小值;
②若![]() ,則
,則
|
|
|
| - | - |
| 遞減 | 遞減 |
此時(shí)![]() 時(shí)無極小值;
時(shí)無極小值;
③若![]() ,則
,則
|
|
|
| 0 |
|
| - | 0 | + | 0 | - |
| 遞減 | 極小值 | 遞增 | 極大值 | 遞減 |
此時(shí)![]() 時(shí)為極大值,
時(shí)為極大值,
綜上所述必須,![]() ,而
,而![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
故![]()


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某超市經(jīng)營一批產(chǎn)品,在市場銷售中發(fā)現(xiàn)此產(chǎn)品在30天內(nèi)的日銷售量P(件)與日期![]() )之間滿足
)之間滿足![]() ,已知第5日的銷售量為55件,第10日的銷售量為50件。
,已知第5日的銷售量為55件,第10日的銷售量為50件。
(1)求第20日的銷售量; (2)若銷售單價(jià)Q(元/件)與![]() 的關(guān)系式為
的關(guān)系式為![]() ,求日銷售額
,求日銷售額![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)函數(shù)![]() 在定義域內(nèi)存在零點(diǎn),求
在定義域內(nèi)存在零點(diǎn),求![]() 的取值范圍.
的取值范圍.
(3)若![]() ,當(dāng)
,當(dāng)![]() 時(shí),不等式
時(shí),不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .(Ⅰ)求函數(shù)
.(Ⅰ)求函數(shù)![]() 的最小正周期及單調(diào)遞增區(qū)間;(Ⅱ)將
的最小正周期及單調(diào)遞增區(qū)間;(Ⅱ)將![]() 的圖像向右平移
的圖像向右平移![]() 個(gè)單位得到函數(shù)
個(gè)單位得到函數(shù)![]() 的圖像,若
的圖像,若![]() ,求函數(shù)
,求函數(shù)![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,公園有一塊邊長為![]() 的等邊
的等邊![]() 的邊角地,現(xiàn)修成草坪,圖中
的邊角地,現(xiàn)修成草坪,圖中![]() 把草坪分成面積相等的兩部分,
把草坪分成面積相等的兩部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)設(shè)![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)如果![]() 是灌溉水管,為節(jié)約成本,希望它最短,
是灌溉水管,為節(jié)約成本,希望它最短,![]() 的位置應(yīng)在哪里?如果
的位置應(yīng)在哪里?如果![]() 是參觀線路,則希望它最長,
是參觀線路,則希望它最長,![]() 的位置又應(yīng)在哪里?請說明理由.
的位置又應(yīng)在哪里?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若某產(chǎn)品的直徑長與標(biāo)準(zhǔn)值的差的絕對值不超過1mm時(shí),則視為合格品,否則視為不合格品.在近期一次產(chǎn)品抽樣檢查中,從某廠生產(chǎn)的此種產(chǎn)品中,隨機(jī)抽取5000件進(jìn)行檢測,結(jié)果發(fā)現(xiàn)有50件不合格品.計(jì)算這50件不合格品的直徑長與標(biāo)準(zhǔn)值的差(單位:mm),將所得數(shù)據(jù)分組,得到如下頻率分布表:
分 組 | 頻 數(shù) | 頻 率 |
[-3,-2) | 0.10 | |
[-2,-1) | 8 | |
(1,2] | 0.50 | |
(2,3] | 10 | |
(3,4] | ||
合計(jì) | 50 | 1.00 |
(1)將上面表格中缺少的數(shù)據(jù)填充完整.
(2)估計(jì)該廠生產(chǎn)的此種產(chǎn)品中,不合格品的直徑長與標(biāo)準(zhǔn)值的差落在區(qū)間(1,3]內(nèi)的概率.
(3)現(xiàn)對該廠這種產(chǎn)品的某個(gè)批次進(jìn)行檢查,結(jié)果發(fā)現(xiàn)有20件不合格品.據(jù)此估算這批產(chǎn)品中的合格品的件數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高二(1)班的一次數(shù)學(xué)測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,且將全班25人的成績記為![]() 由右邊的程序運(yùn)行后,輸出
由右邊的程序運(yùn)行后,輸出![]() .據(jù)此解答如下問題:
.據(jù)此解答如下問題:
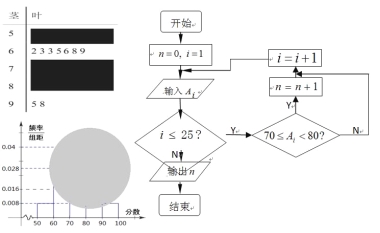
(Ⅰ)求莖葉圖中破損處分?jǐn)?shù)在[50,60),[70,80),[80,90)各區(qū)間段的頻數(shù);
(Ⅱ)利用頻率分布直方圖估計(jì)該班的數(shù)學(xué)測試成績的眾數(shù),中位數(shù)分別是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系中, 以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系, 已知點(diǎn)
軸的非負(fù)半軸為極軸建立極坐標(biāo)系, 已知點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 為參數(shù)).
為參數(shù)).
(1)直線![]() 過
過![]() 且與曲線
且與曲線![]() 相切, 求直線
相切, 求直線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對稱, 求曲線
軸對稱, 求曲線![]() 上的點(diǎn)到點(diǎn)
上的點(diǎn)到點(diǎn)![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國象棋中規(guī)定:馬走“日”字,象走“田”字.如下圖,在中國象棋的半個(gè)棋盤(![]() 的矩形中每個(gè)小方格都是單位正方形)中,若馬在
的矩形中每個(gè)小方格都是單位正方形)中,若馬在![]() 處,可跳到
處,可跳到![]() 處,也可跳到
處,也可跳到![]() 處,用向量
處,用向量![]() ,
,![]() 表示馬走了“一步”.通過探究,你能在圖中畫出馬在
表示馬走了“一步”.通過探究,你能在圖中畫出馬在![]() 處走了一步的所有情況嗎?
處走了一步的所有情況嗎?

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com