
【題目】某早餐店每天制作甲、乙兩種口味的糕點共n(nN*)份,每份糕點的成本1元,售價2元,如果當天賣不完,剩下的糕點作廢品處理.該早餐店發現這兩種糕點每天都有剩余,為此整理了過往100天這兩種糕點的日銷量(單位:份),得到如下的統計數據:
甲口味糕點日銷量 | 48 | 49 | 50 | 51 |
天數 | 20 | 40 | 20 | 20 |
乙口味糕點日銷量 | 48 | 49 | 50 | 51 |
天數 | 40 | 30 | 20 | 10 |
以這100天記錄的各銷量的頻率作為各銷量的概率,假設這兩種糕點的日銷量相互獨立.
(1)記該店這兩種糕點每日的總銷量為X份,求X的分布列
(2)早餐店為了減少浪費,提升利潤,決定調整每天制作糕點的份數
①若產生浪費的概率不超過0.6,求n的最大值;
②以銷售這兩種糕點的日總利潤的期望值為決策依據,在每天所制糕點能全部賣完與n=98之中選其一,應選哪個?
【答案】(1)見解析;(2)![]() ,98.
,98.
【解析】試題分析:(1)由題意知![]() 的可能取值為
的可能取值為![]() 分別求出相應的概率,由此能求出
分別求出相應的概率,由此能求出![]() 分布列;(2)①求出
分布列;(2)①求出![]() ,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部賣完時,
,由此能求出n的最大值; ②由(1)知在每天所制蛋糕能全部賣完時, ![]() ,此時銷售這兩種糕點的日總利潤的期望值為
,此時銷售這兩種糕點的日總利潤的期望值為![]() ,再求出當
,再求出當![]() 時,銷售這兩種糕點的日總利潤的期望值,由此得到應選
時,銷售這兩種糕點的日總利潤的期望值,由此得到應選![]() .
.
試題解析:(1)X所有可能的取值為96,97,98,99,100,101,102
P(X=96)=0.20.4=0.08
P(X=97)=0.20.3+0.40.4=0.22
P(X=98)= 0.20.2+0.40.3+0.20.4=0.24
P(X=99)= 0.20.1+0.40.2+0.20.3+0.20.4=0.24
P(X=100)= 0.40.1+0.20.2+0.20.3=0.14
P(X=101)= 0.20.1+0.20.2=0.06
P(X=102)= 0.20.1=0.02
X的分布列
X | 96 | 97 | 98 | 99 | 100 | 101 | 102 |
P | 0.08 | 0.22 | 0.24 | 0.24 | 0.14 | 0.06 | 0.02 |
(2)①依題意得,P(X<n)0.6,由P(X<99)=0.54,P(X<100)=0.78,n99
②記銷售兩種糕點的日總利潤為Y,
當每天所制作糕點能全部賣完時,E(Y)96
當n=98時,E(Y)=(96-2)0.08+(97-1)0.22+980.7=97.24>96
選n=98


科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 對任意的正整數n,都有an=5Sn+1成立,記bn= ![]() (n∈N*).
(n∈N*).
(1)求數列{an}和數列{bn}的通項公式;
(2)設數列{bn}的前n項和為Rn , 求證:對任意的n∈N* , 都有Rn<4n;
(3)記cn=b2n﹣b2n﹣1(n∈N*),設數列{cn}的前n項和為Tn , 求證:對任意n∈N* , 都有Tn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C為△ABC的三個內角,且其對邊分別為a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面積.
,b+c=4,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ),且
),且![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若函數![]() 在區間
在區間![]() 內有且僅有一個極值點,求
內有且僅有一個極值點,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)設![]() (
(![]() )為兩曲線
)為兩曲線![]() (
(![]() ),
),![]() 的交點,且兩曲線在交點
的交點,且兩曲線在交點![]() 處的切線分別為
處的切線分別為![]() ,
, ![]() .若取
.若取![]() ,試判斷當直線
,試判斷當直線![]() ,
, ![]() 與
與![]() 軸圍成等腰三角形時
軸圍成等腰三角形時![]() 值的個數并說明理由.
值的個數并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)=Asin(ωx+φ)(x>0,A>0)的圖象如圖所示. 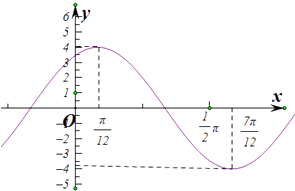
(1)求函數f(x)的解析式;
(2)寫出函數f(x)的單調遞增區間
(3)設不相等的實數,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知如圖所示的程序框圖 
(1)當輸入的x為2,﹣1時,分別計算輸出的y值,并寫出輸出值y關于輸入值x的函數關系式;
(2)當輸出的結果為4時,求輸入的x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題中,正確的有( ) ①兩個變量間的相關系數r越小,說明兩變量間的線性相關程度越低;
②命題“x∈R,使得x2+x+1<0”的否定是:“對x∈R,均有x2+x+1>0”;
③命題“p∧q為真”是命題“p∨q為真”的必要不充分條件;
④若函數f(x)=x3+3ax2+bx+a2在x=﹣1有極值0,則a=2,b=9或a=1,b=3.
A.0 個
B.1 個
C.2 個
D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如下表(假設該區域空氣質量指數不會超過![]() ):
):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 |
|
|
|
|
|
|
該社團將該校區在![]() 年
年![]() 天的空氣質量指數監測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質量指數監測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
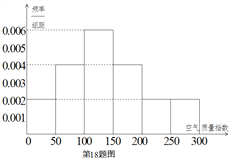
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質量優良的天數(未滿一天按一天計算);
天計算)全年空氣質量優良的天數(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現
日將作為高考考場,若這兩天中某天出現![]() 級重度污染,需要凈化空氣費用
級重度污染,需要凈化空氣費用![]() 元,出現
元,出現![]() 級嚴重污染,需要凈化空氣費用
級嚴重污染,需要凈化空氣費用![]() 元,記這兩天凈化空氣總費用為
元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com