實驗北校舉行運動會，組委會招墓了16名男志愿者和14名女志愿者，調查發現，男、女志愿者中分別有10 人和6人喜愛運動，其余不喜愛.
（1）根據以上數據完成以下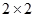
列聯表：
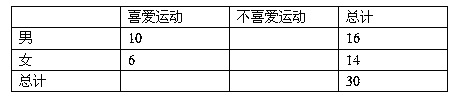
（2）根據列聯表的獨立性檢驗，有多大的把握認為性別與喜愛運動有關？
(3)從不喜愛運動的女志愿者中和喜愛運動的女志愿者中各選1人，求其中不喜愛運動的女生甲及喜愛運動的女生乙至少有一人被選取的概率．
參考公式 ：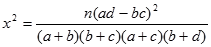
（其中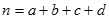
）
| |  |  |  |  |
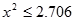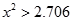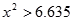| 是否有關聯 | 沒有關聯 | 90% | 95% | 99% |
（1）見解析；（2）性別與喜愛運動沒有關聯；（3）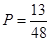
.
解析試題分析：（1）獨立性檢驗關鍵是計算出
,并同概率表作對比，選擇適合的臨界值
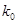，得出是否具有相關性結論；（2）古典概型概率的計算，間接法：“1”減去既沒有甲乙的概率.
試題解析：（1）由已知得：
（2）由已知得： 喜愛運動 不喜愛運動 總計 男 10 6 16 女 6 8 14 總計 16 14 30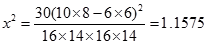 
，則：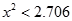
（選擇第一個）.
則：性別與喜愛運動沒有關聯. 8分
（3）記不喜愛運動的女生甲及喜愛運動的女生乙至少有一人被選取為事件A，由已知得：從不喜愛運動的女志愿者中和喜愛運動的女志愿者中各抽取1人共有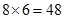
種方法，其中不喜愛運動的女生甲及喜愛運動的女生乙沒有一人被選取的共有
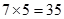種方法，則：
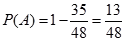12分
考點：（1）獨立性檢測；（2）古典概型.
科目：高中數學 來源： 題型：解答題
設有關于
的一元二次方程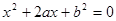
(1)若
是從0,1,2,3四個數中任取的一個數，
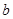是從0,1,2三個數中任取的一個數，求上述方程有實根的概率；
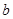(2)若是從區間[0,3]任取的一個數，是從區間[0,2]任取的一個數，求上述方程有實根的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
一個布袋里有3個紅球，2個白球共５個球. 現抽取3次，每次任意抽取2個，并待放回后再抽下一次.求：
（1）３次抽取中，每次取出的2個球都是1個白球和1個紅球的概率；
（2）３次抽取中，有2次取出的2個球是1個白球和1個紅球，還有1次取出的2個球同色的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
現有編號分別為1，2，3，4，5的五個不同的語文題和編號分別為6，7，8，9，的四個不同的數學題。甲同學從這九個題中一次隨機抽取兩道題，每題被抽到的概率是相等的，用符號（x，y）表示事件“抽到的兩題的編號分別為x、y，且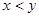
”
（1）共有多少個基本事件？并列舉出來；
（2）求甲同學所抽取的兩題的編號之和小于17但不小于11的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
有甲、乙兩個班進行數學考試，按照大于或等于85分為優秀，85分以下為非優秀統計成績后，得到如下的2×2列聯表：
| | 優秀 | 非優秀 | 總計 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 總計 | | | 210 |
．
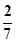，其中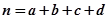
.| 參考數據 | 當 ≤2.706時，無充分證據判定變量A，B有關聯，可以認為兩變量無關聯； |
| 當＞2.706時，有90%的把握判定變量A，B有關聯； | |
| 當＞3.841時，有95%的把握判定變量A，B有關聯； | |
| 當＞6.635時，有99%的把握判定變量A，B有關聯． |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
現有10道題，其中6道甲類題，4道乙類題，張同學從中任取3道題解答．
（1）求張同學至少取到1道乙類題的概率；
（2）已知所取的3道題中有2道甲類題，1道乙類題．設張同學答對每道甲類題的概率都是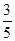
，答對每道乙類題的概率都是
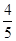，且各題答對與否相互獨立．用
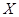表示張同學答對題的個數，求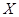的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某大學志愿者協會有6名男同學，4名女同學．在這10名同學中，3名同學來自數學學院，其余7名同學來自物理、化學等其他互不相同的七個學院．現從這10名同學中隨機選取3名同學，到希望小學進行支教活動（每位同學被選到的可能性相同）．
（1）求選出的3名同學是來自互不相同學院的概率；
（2）設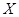
為選出的3名同學中女同學的人數，求隨機變量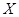的分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，乙出現的點數為
，若令
為
的概率，
為
的概率，試求
的值.
，從中任意摸出2個球，得到的都是白球的概率為