
【題目】如圖(1),在等腰梯形![]() 中,
中, ![]() ,
, ![]() 是梯形的高,
是梯形的高, ![]() ,
, ![]() ,現(xiàn)將梯形沿
,現(xiàn)將梯形沿![]() ,
, ![]() 折起,使
折起,使![]() 且
且![]() ,得一簡(jiǎn)單組合體
,得一簡(jiǎn)單組合體![]() 如 圖(2)示,已知
如 圖(2)示,已知![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點(diǎn).
的中點(diǎn).

(1)求證: ![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角大小.
所成的銳二面角大小.
【答案】(1)證明見(jiàn)解析;(2)![]() .
.
【解析】試題分析:
(1)利用題意結(jié)合幾何關(guān)系可得: ![]() ,結(jié)合線面平行的判斷定理可得:
,結(jié)合線面平行的判斷定理可得: ![]() 平面
平面![]() .
.
(2)利用題意建立空間直角坐標(biāo)系,求得平面![]() 與平面
與平面![]() 的法向量,據(jù)此可得平面
的法向量,據(jù)此可得平面![]() 與平面
與平面![]() 所成銳二面角的大小為
所成銳二面角的大小為![]() .
.
試題解析:
(1)連![]() ,∵四邊形
,∵四邊形![]() 是矩形,
是矩形, ![]() 為
為![]() 中點(diǎn),∴
中點(diǎn),∴![]() 為
為![]() 中點(diǎn),
中點(diǎn),
在![]() 中,
中, ![]() 為
為![]() 中點(diǎn),故
中點(diǎn),故![]() ,又∵
,又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.


(2)依題意知![]() ,
, ![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,
,
∴![]() 在面
在面![]() 上的射影是
上的射影是![]() ,∴
,∴![]() 為
為![]() 與平面
與平面![]() 所成的角,
所成的角,
∴![]() ,∴
,∴![]() ,
, ![]() ,
,
設(shè)![]() 且
且![]() ,分別以
,分別以![]() ,
, ![]() ,
, ![]() 所在的直線為
所在的直線為![]() ,
, ![]() ,
, ![]() 軸建立空間直角坐標(biāo)系,
軸建立空間直角坐標(biāo)系,
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
設(shè)![]() ,
, ![]() 分別是平面
分別是平面![]() 與平面
與平面![]() 的法向量
的法向量
令![]() ,
, ![]() ,即
,即 ,
,  ,
,
取![]() ,
, ![]() ,則
,則![]() ,∴平面
,∴平面![]() 與平面
與平面![]() 所成銳二面角的大小為
所成銳二面角的大小為![]() .
.


 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖在△ABC中,已知點(diǎn)D在BC邊上,滿足AD⊥AC,cos ∠BAC=-![]() ,AB=3
,AB=3![]() ,BD=
,BD=![]() .
.
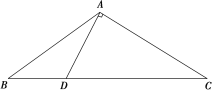
(1)求AD的長(zhǎng);
(2)求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】關(guān)于函數(shù)![]() 有下列命題:
有下列命題:
①函數(shù)![]() 的圖象關(guān)于
的圖象關(guān)于![]() 軸對(duì)稱(chēng);
軸對(duì)稱(chēng);
②在區(qū)間![]() 上,函數(shù)
上,函數(shù)![]() 是減函數(shù);
是減函數(shù);
③在區(qū)間![]() 上,函數(shù)
上,函數(shù)![]() 是增函數(shù);
是增函數(shù);
④函數(shù)![]() 的值域是
的值域是![]() .其中正確命題序號(hào)為____.
.其中正確命題序號(hào)為____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() 為實(shí)數(shù).
為實(shí)數(shù).
(1)若關(guān)于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最小值(用
的最小值(用![]() 表示);
表示);
(3)若關(guān)于![]() 不等式
不等式![]() 的解集中恰好有兩個(gè)整數(shù)解,求
的解集中恰好有兩個(gè)整數(shù)解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】近年來(lái),空氣質(zhì)量成為人們?cè)絹?lái)越關(guān)注的話題,空氣質(zhì)量指數(shù)(![]() ,簡(jiǎn)稱(chēng)
,簡(jiǎn)稱(chēng)![]() )是定量描述空氣質(zhì)量狀況的指數(shù),空氣質(zhì)量按照
)是定量描述空氣質(zhì)量狀況的指數(shù),空氣質(zhì)量按照![]() 大小分為六級(jí),
大小分為六級(jí), ![]() 為優(yōu);
為優(yōu); ![]() 為良;
為良; ![]() 為輕度污染;
為輕度污染; ![]() 為中度污染;
為中度污染; ![]() 為重度污染;大于300為嚴(yán)重污染.環(huán)保部門(mén)記錄了2017年某月哈爾濱市10天的
為重度污染;大于300為嚴(yán)重污染.環(huán)保部門(mén)記錄了2017年某月哈爾濱市10天的![]() 的莖葉圖如下:
的莖葉圖如下:

(1)利用該樣本估計(jì)該地本月空氣質(zhì)量?jī)?yōu)良(![]() )的天數(shù);(按這個(gè)月總共30天計(jì)算)
)的天數(shù);(按這個(gè)月總共30天計(jì)算)
(2)現(xiàn)工作人員從這10天中空氣質(zhì)量為優(yōu)良的日子里隨機(jī)抽取2天進(jìn)行某項(xiàng)研究,求抽取的2天中至少有一天空氣質(zhì)量是優(yōu)的概率;
(3)將頻率視為概率,從本月中隨機(jī)抽取3天,記空氣質(zhì)量?jī)?yōu)良的天數(shù)為![]() ,求
,求![]() 的概率分布列和數(shù)學(xué)期望.
的概率分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】齊王與田忌賽馬,田忌的上等馬優(yōu)于齊王的中等馬,劣于齊王的上等馬,田忌的中等馬優(yōu)于齊王的下等馬,劣于齊王的中等馬,田忌的下等馬劣于齊王的下等馬,現(xiàn)從雙方的馬匹中隨機(jī)選一匹進(jìn)行一場(chǎng)比賽,則田忌馬獲勝的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=![]() .(a>0)
.(a>0)
(1)若a=1,證明:y=f(x)在R上單調(diào)遞減;
(2)當(dāng)a>1時(shí),討論f(x)零點(diǎn)的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)求證: ![]() .
.
(2)某同學(xué)在一次研究性學(xué)習(xí)中發(fā)現(xiàn),以下五個(gè)式子的值都等于同一個(gè)常數(shù):
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①試從上述五個(gè)式子中選擇一個(gè),求出這個(gè)常數(shù);
②根據(jù)①的計(jì)算結(jié)果,將該同學(xué)的發(fā)現(xiàn)推廣為三角恒等式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,l是過(guò)定點(diǎn)P(4,2)且傾斜角為α的直線;在極坐標(biāo)系(以坐標(biāo)原點(diǎn)O為極點(diǎn),
以x軸非負(fù)半軸為極軸,取相同單位長(zhǎng)度)中,曲線C的極坐標(biāo)方程為![]() .
.
(1)寫(xiě)出直線l的參數(shù)方程,并將曲線C的方程化為直角坐標(biāo)方程;
(2)若曲線C與直線相交于不同的兩點(diǎn)M,N,求|PM|+|PN|的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com