
【題目】在△ABC中,角A、B、C所對的邊分別為a、b、c,f (x)=sin(2x﹣A) (x∈R),函數f(x)的圖象關于點( ![]() ,0)對稱.
,0)對稱.
(1)當x∈(0, ![]() )時,求f (x)的值域;
)時,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面積.
,求△ABC的面積.
【答案】
(1)解:∵函數f(x)的圖象關于點( ![]() ,0)對稱,
,0)對稱,
∴f( ![]() )=0,即sin(2×
)=0,即sin(2× ![]() ﹣A)=0.
﹣A)=0.
又A∈(0,π),
∴A= ![]() .
.
∵x∈(0, ![]() ),
),
∴2x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),
),
∴﹣ ![]() <sin(2x﹣
<sin(2x﹣ ![]() )≤1,
)≤1,
即函數f(x)的值域為(﹣ ![]() ,1].
,1].
(2)解:由正弦定理 ![]() ,
,
得sinB+sinC= ![]() +
+ ![]() ,
,
又∵a=7,A= ![]() ,
,
∴sinB+sinC= ![]() (b+c).
(b+c).
∵sinB+sinC= ![]() ,
,
∴b+c=13.
由余弦定理a2=b2+c2﹣2bccosA,
得49=b2+c2﹣bc,
即49=(b+c)2﹣3bc=169﹣3bc,
∴bc=40.
∴S△ABC= ![]() bcsinA=10
bcsinA=10 ![]() .
.
【解析】(1)由題意sin(2× ![]() ﹣A)=0,結合A∈(0,π),可得A=
﹣A)=0,結合A∈(0,π),可得A= ![]() ,由x∈(0,
,由x∈(0, ![]() ),可求2x﹣
),可求2x﹣ ![]() 的范圍,利用正弦函數的圖象和性質即可得解f(x)的值域.(2)由正弦定理得sinB+sinC=
的范圍,利用正弦函數的圖象和性質即可得解f(x)的值域.(2)由正弦定理得sinB+sinC= ![]() +
+ ![]() ,結合已知可求b+c=13,利用余弦定理可求bc的值,利用三角形面積公式即可得解.
,結合已知可求b+c=13,利用余弦定理可求bc的值,利用三角形面積公式即可得解.
【考點精析】通過靈活運用正弦定理的定義和余弦定理的定義,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此題.
即可以解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,底面四邊形ABCD是菱形,
中,底面四邊形ABCD是菱形, ![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形, ![]() ,
, ![]() .
.
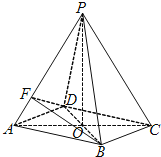
![]() Ⅰ
Ⅰ![]() 求證:
求證: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直線CP與平面BDF所成角的大小;
求直線CP與平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在線段PB上是否存在一點M,使得
在線段PB上是否存在一點M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,請說明理由.
的值,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() =
=
(1)寫出該函數的單調區間;
(2)若函數![]() =
=![]() -m恰有3個不同零點,求實數m的取值范圍;
-m恰有3個不同零點,求實數m的取值范圍;
(3)若![]() ≤n2-2bn+1對所有x∈[-1,1],b∈[-1,1]恒成立,求實數n的取值范圍.
≤n2-2bn+1對所有x∈[-1,1],b∈[-1,1]恒成立,求實數n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩名學生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現這兩名學生在相同條件下各射箭10次,命中的環數如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環數的平均數和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學生參加射箭比賽.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側棱垂直于底面,
中,側棱垂直于底面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:在棱![]() 上存在一點
上存在一點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線C:x2=2py(p>0)的焦點為F,準線為l,A為C上一點,已知以F為圓心,FA為半徑的圓F交l于B,D兩點.
(1)若p=2且∠BFD=90°時,求圓F的方程;
(2)若A,B,F三點在同一直線m上,設直線m與拋物線C的另一個交點為E,在y軸上求一點G,使得∠OGE=∠OGA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
: ![]() 的離心率
的離心率![]() ,短軸右端點為
,短軸右端點為![]() ,
, ![]() 為線段
為線段![]() 的中點.
的中點.
(Ⅰ) 求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 任作一條直線與橢圓
任作一條直線與橢圓![]() 相交于兩點
相交于兩點![]() ,試探究在
,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com