
【題目】已知不等式組 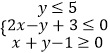 表示的平面區(qū)域為D,若(x,y)∈D,|x|+2y≤a為真命題,則實(shí)數(shù)a的取值范圍是( )
表示的平面區(qū)域為D,若(x,y)∈D,|x|+2y≤a為真命題,則實(shí)數(shù)a的取值范圍是( )
A.[10,+∞)
B.[11,+∞)
C.[13,+∞)
D.[14,+∞)
【答案】D
【解析】解:不等式組 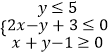 表示的平面區(qū)域為D,如圖: 當(dāng)x≥0時,z=|x|+2y=x+2y,z=x+2y經(jīng)過B時取得最大值,
表示的平面區(qū)域為D,如圖: 當(dāng)x≥0時,z=|x|+2y=x+2y,z=x+2y經(jīng)過B時取得最大值,
由 ![]() 可得B(1,5),此時z的最大值為:11.
可得B(1,5),此時z的最大值為:11.
當(dāng)x<0時,z=|x|+2y=﹣x+2y,z=﹣x+2y經(jīng)過A時取得最大值,
由 ![]() ,可得A(﹣4,5),此時z的最大值為:14.
,可得A(﹣4,5),此時z的最大值為:14.
若(x,y)∈D,|x|+2y≤a為真命題,則實(shí)數(shù)a的取值范圍:[14,+∞).
故選:D.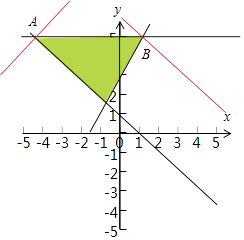
【考點(diǎn)精析】利用命題的真假判斷與應(yīng)用對題目進(jìn)行判斷即可得到答案,需要熟知兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關(guān)系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠為了對新研發(fā)的一種產(chǎn)品進(jìn)行合理定價,將該產(chǎn)品按事先擬定的價格進(jìn)行試銷,得到如下數(shù)據(jù):
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =﹣20,
=﹣20, ![]() =
= ![]() ﹣
﹣ ![]()
![]()
(2)預(yù)計在今后的銷售中,銷量與單價仍然服從(1)中的關(guān)系,且該產(chǎn)品的成本是4元/件,為使工廠獲得最大利潤,該產(chǎn)品的單價應(yīng)定為多少元?(利潤=銷售收入﹣成本)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在三棱錐P﹣ABC中,PA⊥平面ABC,AC⊥BC,D為側(cè)棱PC上一點(diǎn),它的正(主)視圖和側(cè)(左)視圖如圖2所示. 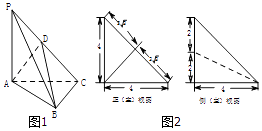
(1)證明:AD⊥BC;
(2)求三棱錐D﹣ABC的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0,設(shè)命題p:函數(shù)y=ax在R上單調(diào)遞增;命題q:不等式ax2﹣ax+1>0對x∈R恒成立,若p且q為假,p或q為真,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2 ![]() ,PA⊥AB.
,PA⊥AB. 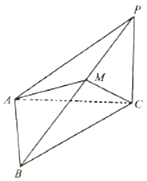
(1)求PC的長;
(2)若點(diǎn)M在側(cè)棱PB上,且 ![]() ,當(dāng)λ為何值時,二面角B﹣AC﹣M的大小為30°.
,當(dāng)λ為何值時,二面角B﹣AC﹣M的大小為30°.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在我國古代著名的數(shù)學(xué)專著《九章算術(shù)》里有﹣段敘述:今有良馬與駑馬發(fā)長安至齊,齊去長安一千一百二十五里,良馬初日行一百零三里,日增十三里:駑馬初日行九十七里,日減半里,良馬先至齊,復(fù)還迎駑馬,二馬相逢, 問:需日相逢.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北京、張家港2022年冬奧會申辦委員會在俄羅斯索契舉辦了發(fā)布會,某公司為了競標(biāo)配套活動的相關(guān)代言,決定對旗下的某商品進(jìn)行一次評估.該商品原來每件售價為25元,年銷售8萬件.
(1)據(jù)市場調(diào)查,若價格每提高1元,銷售量將相應(yīng)減少2000件,要使銷售的總收入不低于原收入,該商品每件定價最多為多少元?
(2)為了抓住申奧契機(jī),擴(kuò)大該商品的影響力,提高年銷售量.公司決定立即對該商品進(jìn)行全面技術(shù)革新和營銷策略改革,并提高定價到x元.公司擬投入 ![]() 萬作為技改費(fèi)用,投入(50+2x)萬元作為宣傳費(fèi)用.試問:當(dāng)該商品改革后的銷售量a至少應(yīng)達(dá)到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
萬作為技改費(fèi)用,投入(50+2x)萬元作為宣傳費(fèi)用.試問:當(dāng)該商品改革后的銷售量a至少應(yīng)達(dá)到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=sin(2x+ ![]() )+
)+ ![]() cos(2x+
cos(2x+ ![]() ),則( )
),則( )
A.y=f(x)在(0, ![]() )單調(diào)遞增,其圖象關(guān)于直線x=
)單調(diào)遞增,其圖象關(guān)于直線x= ![]() 對稱
對稱
B.y=f(x)在(0, ![]() )單調(diào)遞增,其圖象關(guān)于直線x=
)單調(diào)遞增,其圖象關(guān)于直線x= ![]() 對稱
對稱
C.y=f(x)在(0, ![]() )單調(diào)遞減,其圖象關(guān)于直線x=
)單調(diào)遞減,其圖象關(guān)于直線x= ![]() 對稱
對稱
D.y=f(x)在(0, ![]() )單調(diào)遞減,其圖象關(guān)于直線x=
)單調(diào)遞減,其圖象關(guān)于直線x= ![]() 對稱
對稱
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,為測一樹的高度,在地面上選取A、B兩點(diǎn),從A、B兩點(diǎn)分別測得樹尖的仰角為30°、45°,且A、B兩點(diǎn)之間的距離為60m,則樹的高度為( ) 
A.(30+30 ![]() ) m
) m
B.(30+15 ![]() ) m??
) m??
C.(15+30 ![]() ) m
) m
D.(15+15 ![]() ) m
) m
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com