
���}Ŀ����֪����������(bi��o)ԭ�c(di��n)�����c(di��n)��![]() �S�ϵęE�A���x���ʞ�
�S�ϵęE�A���x���ʞ�![]() ���^�c(di��n)
���^�c(di��n)![]() ���^���c(di��n)
���^���c(di��n)![]() �Ą�(d��ng)ֱ���cԓ�E�A�ཻ��
�Ą�(d��ng)ֱ���cԓ�E�A�ཻ��![]() ��
��![]() ���c(di��n).
���c(di��n).
��1��������![]() ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)��![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����![]() �S���Ƿ�����c(di��n)
�S���Ƿ�����c(di��n)![]() ��ʹ
��ʹ![]() �鳣��(sh��)�������ڣ�����c(di��n)
�鳣��(sh��)�������ڣ�����c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f������.
������(bi��o)���������ڣ�Ո(q��ng)�f������.
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������ԇ�}��������1���E�A���x���ʹ�ʽ����![]() ���P(gu��n)ϵ�����
���P(gu��n)ϵ�����![]() ���õ��E�A�ķ��̣��O(sh��)��ֱ��
���õ��E�A�ķ��̣��O(sh��)��ֱ��![]() �ķ��̣���ֱ�����̴���E�A�������������f�_(d��)����������ʾ�����c(di��n)����(bi��o)���˕r(sh��)������֪
�ķ��̣���ֱ�����̴���E�A�������������f�_(d��)����������ʾ�����c(di��n)����(bi��o)���˕r(sh��)������֪![]() ���c(di��n)�ęM����(bi��o)���������ֱ��
���c(di��n)�ęM����(bi��o)���������ֱ��![]() �ķ��̣���2�����O(sh��)�����c(di��n)
�ķ��̣���2�����O(sh��)�����c(di��n)![]() ��ʹ
��ʹ![]() �鳣��(sh��)���քe�֮�(d��ng)
�鳣��(sh��)���քe�֮�(d��ng)![]() �c
�c![]() �S����ֱ�r(sh��)�Լ���(d��ng)ֱ��
�S����ֱ�r(sh��)�Լ���(d��ng)ֱ��![]() �c
�c![]() �S��ֱ�r(sh��)������c(di��n)
�S��ֱ�r(sh��)������c(di��n)![]() ������(bi��o)�����C�σɷN��r�ó��Y(ji��)Փ��
������(bi��o)�����C�σɷN��r�ó��Y(ji��)Փ��
ԇ�}��������1������E�A�ķ��̞�![]() ��
��
ֱ��б�ʲ����ڕr(sh��)�@Ȼ���������O(sh��)ֱ��![]() ��
��
��![]() ����E�A�ķ���
����E�A�ķ���![]() ��
��
��ȥ![]() ������
������![]() ��
��
�O(sh��)![]() ���t
���t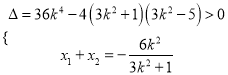 ��
��
��?y��n)龀��![]() �����c(di��n)�ęM����(bi��o)��
�����c(di��n)�ęM����(bi��o)��![]() �����
�����![]() ��
��
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��2�����O(sh��)��![]() �S�ϴ����c(di��n)
�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �鳣��(sh��)��
�鳣��(sh��)��
����(d��ng)ֱ��![]() �c
�c![]() �S����ֱ�r(sh��)���ɣ�1��֪
�S����ֱ�r(sh��)���ɣ�1��֪![]() ��
��
����![]()
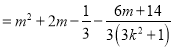 ��
��
��?y��n)?/span>![]() ���c
���c![]() �o�P(gu��n)�ij���(sh��)���Ķ���
�o�P(gu��n)�ij���(sh��)���Ķ���![]() ��
��
�˕r(sh��)![]()
����(d��ng)ֱ��![]() �c
�c![]() �S��ֱ�r(sh��)���˕r(sh��)�Y(ji��)Փ������
�S��ֱ�r(sh��)���˕r(sh��)�Y(ji��)Փ������
�C�Ͽ�֪����![]() �S�ϴ��ڶ��c(di��n)
�S�ϴ��ڶ��c(di��n)![]() ��ʹ
��ʹ![]() ���鳣��(sh��)
���鳣��(sh��)


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��ԓ����(sh��)�D���^�c(di��n)
��ԓ����(sh��)�D���^�c(di��n)![]() ���c�c(di��n)
���c�c(di��n)![]() ��������(sh��)�D���ϵ�һ��(g��)����c(di��n)��
��������(sh��)�D���ϵ�һ��(g��)����c(di��n)��![]() ��
��
��1����ԓ����(sh��)�Ľ���ʽ![]() ��
��
��2����(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ���ֵ���䌦(du��)��(y��ng)����׃��
�ϵ���ֵ���䌦(du��)��(y��ng)����׃��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��˾�^ȥ�傀(g��)�µďV���M(f��i)֧��![]() �c�N���~
�c�N���~![]() ����λ���fԪ��֮�g�����Ќ�(du��)��(y��ng)��(sh��)��(j��)��
����λ���fԪ��֮�g�����Ќ�(du��)��(y��ng)��(sh��)��(j��)��
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
�����ˆT������������![]() �ĵ�һ��(g��)��(sh��)��(j��)�Gʧ����֪
�ĵ�һ��(g��)��(sh��)��(j��)�Gʧ����֪![]() ��(du��)
��(du��)![]() �ʾ������P(gu��n)�P(gu��n)ϵ���һؚw���̞�
�ʾ������P(gu��n)�P(gu��n)ϵ���һؚw���̞�![]() ���t�����f�������N���~
���t�����f�������N���~![]() �c�V���M(f��i)֧��
�c�V���M(f��i)֧��![]() �����P(gu��n)�����Gʧ�Ĕ�(sh��)��(j��)������
�����P(gu��n)�����Gʧ�Ĕ�(sh��)��(j��)������![]() ̎����30����ԓ��˾�V���M(f��i)֧��ÿ����1�fԪ���N���~һ������
̎����30����ԓ��˾�V���M(f��i)֧��ÿ����1�fԪ���N���~һ������![]() �fԪ������ԓ��˾���V��Ͷ��8�fԪ���t�N��
�fԪ������ԓ��˾���V��Ͷ��8�fԪ���t�N��
�~��70�fԪ�����У����_�f���У� ��
A��1��(g��) B��2��(g��) C��3��(g��) D��4��(g��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ�У�������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)�� ![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ.��֪�c(di��n)
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ.��֪�c(di��n)![]() �ĘO����(bi��o)��
�ĘO����(bi��o)��![]() ������
������![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() �酢��(sh��)��.
�酢��(sh��)��.
��1��ֱ��![]() �^
�^![]() ���c����
���c����![]() ���У���ֱ��
���У���ֱ��![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2���c(di��n)![]() �c�c(di��n)
�c�c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q��������
�S��(du��)�Q��������![]() �ϵ��c(di��n)���c(di��n)
�ϵ��c(di��n)���c(di��n)![]() �ľ��x��ȡֵ����.
�ľ��x��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪![]() ������(sh��)
������(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)���ⲻ��ʽ
�r(sh��)���ⲻ��ʽ![]() ��
��
��2�����P(gu��n)��![]() �ķ���
�ķ���![]() �Ľ⼯��ǡ��һ��(g��)Ԫ�أ���
�Ľ⼯��ǡ��һ��(g��)Ԫ�أ���![]() ��ȡֵ������
��ȡֵ������
��3���O(sh��)![]() ����(du��)����
����(du��)����![]() ������(sh��)
������(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ����ֵ�c��Сֵ�IJ���^1����
�ϵ����ֵ�c��Сֵ�IJ���^1����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵxOy�У���֪�AC����x��2��2+��y+1��2=5���^�c(di��n)P��5��0����б�ʞ�k��ֱ��![]() �c�AC�ཻ�ڲ�ͬ�ă��c(di��n)A��B��
�c�AC�ཻ�ڲ�ͬ�ă��c(di��n)A��B��
��I����k��ȡֵ������
���������L(zh��ng)|AB|=4����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������˽�ij���W(xu��)���ĕ�(hu��)���ϸ��ʣ�Ҫ��ԓ��70�����x30���M(j��n)�п���������t70�˵ĕ�(hu��)���ɿ�(j��)��ȫ�w��______���ӱ���______���ӱ�����______.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(du��)�ں�(ji��n)���S�C(j��)��ӣ������f�����_���ǣ� ��
����Ҫ��ȡ�ӱ��Ŀ��w�Ă�(g��)�w��(sh��)���ޣ�
�����ǏĿ��w������(g��)�M(j��n)�г�ȡ�ģ��ڌ�(sh��)�`�в�������Ҳ���^���㣻
������һ�N���Żس�ӣ�
������һ�N�ȿ��ܳ�ӣ�������(g��)����^���У�ÿ��(g��)��(g��)�w���鵽�ęC(j��)��(hu��)��ȣ��Ķ����C���@�N��ӷ����Ĺ�ƽ��.
A.�٢ڢ�B.�٢ڢ�C.�٢ۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�ЌW(xu��)��һŮ������450�ˣ������˽��һŮ����������r���S�C(j��)��ȡ���ָ�һŮ���y(c��)�����ߣ����Ô�(sh��)��(j��)�������г��l�ʷֲ������£�
�M�e | �l��(sh��) | �l�� |
145.5��149.5 | 8 | 0.16 |
149.5��153.5 | 6 | 0.12 |
153.5��157.5 | 14 | 0.28 |
157.5��161.5 | 10 | 0.20 |
161.5��165.5 | 8 | 0.16 |
165.5��169.5 |
|
|
��Ӌ(j��) |
|
|
��1�����������ĸ![]() ����(du��)��(y��ng)�Ĕ�(sh��)ֵ��
����(du��)��(y��ng)�Ĕ�(sh��)ֵ��
��2���ڽo����ֱ������(bi��o)ϵ�Ю����l�ʷֲ�ֱ���D��
��3����Ӌ(j��)ԓУ��һŮ��������149.5��165.5![]() ������(n��i)�ж����ˣ�
������(n��i)�ж����ˣ�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com