Question

【題目】已知函數，函數的圖像為直線．

（Ⅰ）當時，若函數的圖像永遠在直線下方，求實數的取值范圍；

（Ⅱ）當時，若直線與函數的圖像的有兩個不同的交點，線段的中點為 ，求證：．

Answer 1

【答案】（1）的取值范圍是；（2）見解析.

【解析】

（1）當時，若函數的圖像永遠在直線下方，轉化為在上恒成立上，設，利用導數得到在時取得最大值，即可求解實數的取值范圍；

（2）設的橫坐標是，要證，轉化為證，

不妨設，則，轉化為證明，進而轉化為即證，令，等價于證明在時恒成立. 構造新函數，利用導數求得函數的單調性與最值，即可得到結論．

（1）當時，若函數的圖像永遠在直線下方，即，

在上恒成立，即在上恒成立上．

設，對求導得 ，

, ，

所以在時取得極大值，也是最大值，于是的取值范圍是．

（2）設的橫坐標是（不妨設)，

要證，只需證，即證，

即證， 即證，

，只需證明：，

不妨設，則，所以只需證，

即證，只需證，

因為直線與曲線相交，所以,，

所以

則只需證，即證：，即證（※），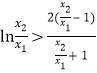

下面構造函數證明之：因為已設，且由的定義域知，，

所以令，則（※）等價于證明在時恒成立.

為此構造函數，則，

于是當時，，即在上遞增，

又，所以在恒成立，即在時恒成立，

則（※）成立，于是原命題成立．