
已知函數 .
.
(I)求函數 的單調區間;
的單調區間;
(II)若函數 上是減函數,求實數
上是減函數,求實數 的最小值;
的最小值;
(III)若 ,使
,使 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
(I) (II)
(II) (III)
(III)
解析試題分析:由已知函數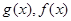 的定義域均為
的定義域均為 ,且
,且 .
.
(Ⅰ)函數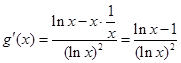 ,
,
當 時,
時,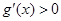 .所以函數
.所以函數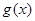 的單調增區間是
的單調增區間是 . 3分
. 3分
(Ⅱ)因f(x)在 上為減函數,故
上為減函數,故 在
在 上恒成立.
上恒成立.
所以當 時,
時,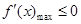 .
.
又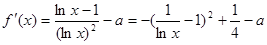 ,
,
故當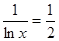 ,即
,即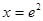 時,
時,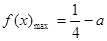 ,所以
,所以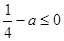 ,故
,故
所以 的最小值為
的最小值為 .
.
(Ⅲ)“若 ,使
,使 成立”等價于
成立”等價于
“當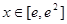 時,有
時,有 ”,
”,
有(Ⅱ),當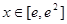 時,有
時,有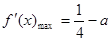 ,
,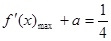 ,
,
問題等價于:“當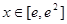 時,有
時,有 ”
” 當
當 時,由(Ⅱ),
時,由(Ⅱ), 在
在 上為減函數.
上為減函數.
則 ,故
,故 .
. 當
當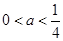 時,由于
時,由于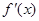
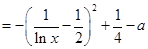 在
在 上為增函數,
上為增函數,
故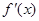 的值域為
的值域為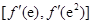 ,即
,即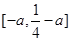 .
.
由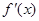 的單調性和值域知,
的單調性和值域知, 唯一
唯一 ,使
,使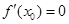 ,且滿足:
,且滿足:
當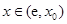 時,
時,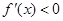 ,
, 為減函數;
為減函數;
當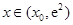 時,
時, ,
, 為增函數;
為增函數;
所以,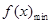 =
=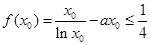 ,
, .
.
所以,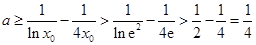 ,與
,與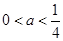 矛盾,不合題意.
矛盾,不合題意.
綜上, .
.
考點:利用導數求閉區間上函數的最值;利用導數研究函數的單調性.
點評:本題考查導數知識的運用,考查函數的單調性與最值,考查恒成立問題,同時考查不等式的證明,解題的關鍵是正確求導數,確定函數的單調性.


科目:高中數學 來源: 題型:解答題
設函數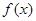 是定義在區間
是定義在區間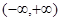 上的偶函數,且滿足
上的偶函數,且滿足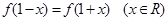
(1)求函數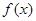 的周期;
的周期;
(2)已知當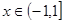 時,
時,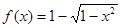 .求使方程
.求使方程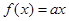 在
在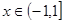 上有兩個不相等實根的
上有兩個不相等實根的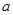 的取值集合M.
的取值集合M.
(3)記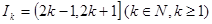 ,
,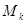 表示使方程
表示使方程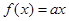 在
在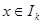 上有兩個不相等實根的
上有兩個不相等實根的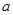 的取值集合,求集合
的取值集合,求集合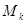 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=x|x-a|-lnx,a∈R.
(Ⅰ)若a=1,求函數f(x)在區間[1,e]上的最大值;
(Ⅱ)若f(x)>0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
若函數 都在區間
都在區間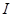 上有定義,對任意
上有定義,對任意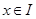 ,都有
,都有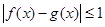 成立,則稱函數
成立,則稱函數 為區間
為區間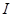 上的“伙伴函數”
上的“伙伴函數”
(1)若 為區間
為區間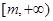 上的“伙伴函數”,求
上的“伙伴函數”,求 的范圍。
的范圍。
(2)判斷 是否為區間
是否為區間 上的“伙伴函數”?
上的“伙伴函數”?
(3)若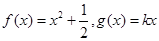 為區間
為區間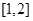 上的“伙伴函數”,求
上的“伙伴函數”,求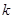 的取值范圍
的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com