
【題目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是
的大小是![]() .連接
.連接![]() ,
,![]() ,如圖:
,如圖:
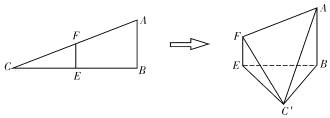
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成二面角的大小.
所成二面角的大小.
【答案】(Ⅰ)證明見解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)法一:由![]() .設
.設![]() 的中點為
的中點為![]() ,連接
,連接![]() .
.
設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,![]() .而
.而![]() 即為二面角
即為二面角![]() 的平面角.
的平面角.
![]() ,推導出
,推導出![]() .由
.由![]() ,
,![]() ,從而
,從而![]() 平面
平面![]() .由
.由![]() ,得
,得![]() 平面
平面![]() ,從而
,從而![]() ,即
,即![]() .進而
.進而![]() 平面
平面![]() .推導出四邊形
.推導出四邊形![]() 為平行四邊形.從而
為平行四邊形.從而![]() ,
,![]() 平面
平面![]() ,由此能證明平面
,由此能證明平面![]() 平面
平面![]() .
.
法二:以![]() 為原點,在平面
為原點,在平面![]() 中過
中過![]() 作
作![]() 的垂線為
的垂線為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,利用向量法能證明平面
軸,建立空間直角坐標系,利用向量法能證明平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 為原點,在平面
為原點,在平面![]() 中過
中過![]() . 作
. 作![]() 的垂線為
的垂線為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,利用向量法能求出平面
軸,建立空間直角坐標系,利用向量法能求出平面![]() 與平面
與平面![]() 所成二面角大小.
所成二面角大小.
(Ⅰ)證法一:![]() 是
是![]() 的中點,
的中點,![]() .
.
設![]() 的中點為
的中點為![]() ,連接
,連接![]() .設
.設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,![]() .
.
由題意得![]() ,
,![]() ,
,
![]() 即為二面角
即為二面角![]() 的平面角.
的平面角.![]() ,
,
![]() 為
為![]() 的中點.
的中點.![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,
,![]() ,即
,即![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.![]() ,
,![]()
四邊形![]() 為平行四邊形.
為平行四邊形.![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.![]() 平面
平面![]() 平面
平面![]() .
.

法二:如圖,以![]() 為原點,
為原點,![]() 為
為![]() 軸,在平面
軸,在平面![]() 中過
中過![]() 作
作![]() 的垂線為
的垂線為![]() 軸,
軸, ![]() 為
為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
設![]() .則
.則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,![]() ,
,![]() ,
,
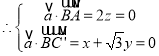 ,令
,令![]() ,則
,則![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
![]() ,
,![]() ,
,
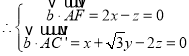 ,取
,取![]() ,得
,得![]() .
.
![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
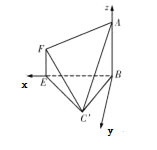
解:(Ⅱ)如圖,以![]() 為原點,
為原點,![]() 為
為![]() 軸,在平面
軸,在平面![]() 中過
中過![]() 作
作![]() 的垂線為
的垂線為![]() 軸,
軸, ![]() 為
為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
設![]() .則
.則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
平面![]() 的法向量
的法向量![]()
設平面![]() 的法向量為
的法向量為![]() ,
,
![]() ,
,![]() ,
,
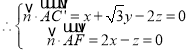 ,取
,取![]() ,得
,得![]() .
.
設平面![]() 與平面
與平面![]() 所成的二面角的平面角為
所成的二面角的平面角為![]() ,
,
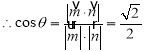
由圖形觀察可知,平面![]() 與平面
與平面![]() 所成的二面角的平面角為銳角.
所成的二面角的平面角為銳角.
![]() 平面
平面![]() 與平面
與平面![]() 所成二面角大小為
所成二面角大小為![]() .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲線C的普通方程;
(2)直線l的參數方程為![]() ,t為參數直線
,t為參數直線![]() 與y軸交于點F與曲線C的交點為A,B,當|FA||FB|取最小值時,求直線
與y軸交于點F與曲線C的交點為A,B,當|FA||FB|取最小值時,求直線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從拋物線![]() 上任意一點P向x軸作垂線段,垂足為Q,點M是線段
上任意一點P向x軸作垂線段,垂足為Q,點M是線段![]() 上的一點,且滿足
上的一點,且滿足![]()
(1)求點M的軌跡C的方程;
(2)設直線![]() 與軌跡c交于
與軌跡c交于![]() 兩點,T為C上異于
兩點,T為C上異于![]() 的任意一點,直線
的任意一點,直線![]() ,
,![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點,以
兩點,以![]() 為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個商場同時出售一款西門子冰箱,其中甲商場位于老城區中心,乙商場位于高新區.為了調查購買者的年齡與購買冰箱的商場選擇是否具有相關性,研究人員隨機抽取了1000名購買此款冰箱的用戶作調研,所得結果如表所示:
50歲以上 | 50歲以下 | |
選擇甲商場 | 400 | 250 |
選擇乙商場 | 100 | 250 |
(1)判斷是否有![]() 的把握認為購買者的年齡與購買冰箱的商場選擇具有相關性;
的把握認為購買者的年齡與購買冰箱的商場選擇具有相關性;
(2)由于乙商場的銷售情況未達到預期標準,商場決定給冰箱的購買者開展返利活動具體方案如下:當天賣出的前60臺(含60臺)冰箱,每臺商家返利200元,賣出60臺以上,超出60臺的部分,每臺返利50元.現將返利活動開展后15天內商場冰箱的銷售情況統計如圖所示:與此同時,老張得知甲商場也在開展返利活動,其日返利額的平均值為11000元,若老張將選擇返利較高的商場購買冰箱,請問老張應當去哪個商場購買冰箱

附: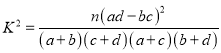 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com