
【題目】已知直三棱柱![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點(diǎn),且
的中點(diǎn),且![]() .
.
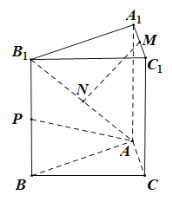
(1)求證:![]() 平面
平面![]() ;
;
(2)求![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,先證明
,先證明![]() ,
,![]() ,從而可得
,從而可得![]() 為平行四邊形,進(jìn)而可得
為平行四邊形,進(jìn)而可得![]() ,再結(jié)合線面平行的判定定理可證明
,再結(jié)合線面平行的判定定理可證明![]() 平面
平面![]() ;
;
(2)設(shè)![]() ,
,![]() ,
,![]() ,
,![]() ,易知
,易知![]() ,且
,且![]() ,進(jìn)而用
,進(jìn)而用![]() 表示出
表示出![]() ,
,![]() ,并結(jié)合
,并結(jié)合![]() ,可求出
,可求出![]() 及
及![]() ;
;
(3)在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 做射線
做射線![]() 垂直于
垂直于![]() ,易知
,易知![]() ,
,![]() ,
,![]() 兩兩垂直,建立如圖所示的空間直角坐標(biāo)系
兩兩垂直,建立如圖所示的空間直角坐標(biāo)系![]() ,進(jìn)而分別求得平面
,進(jìn)而分別求得平面![]() 及平面
及平面![]() 的法向量
的法向量![]() ,
,![]() ,再由
,再由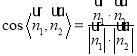 ,可求出二面角
,可求出二面角![]() 的余弦值.
的余弦值.
(1)證明:取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,
則有![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)設(shè)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由已知可得,![]() ,且
,且![]() ,
,
則![]() ,
,![]() ,
,
因?yàn)?/span>![]() ,所以
,所以![]()
![]()
![]() ,
,
所以![]() ,即
,即![]() .
.
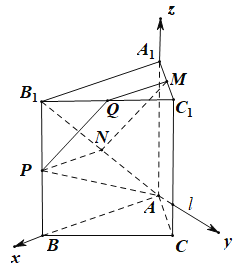
(3)在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 做射線
做射線![]() 垂直于
垂直于![]() ,易知
,易知![]() ,
,![]() ,
,![]() 兩兩垂直,建立如圖所示的空間直角坐標(biāo)系
兩兩垂直,建立如圖所示的空間直角坐標(biāo)系![]() ,
,
則![]() ,
,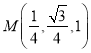 ,
,![]() ,
,
![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
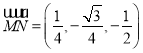 ,
,![]() .
.
設(shè)![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
則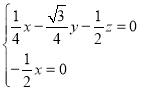 ,令
,令![]() ,則
,則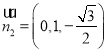 ,
,
則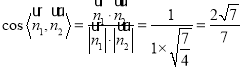 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】輥?zhàn)邮强图覀鹘y(tǒng)農(nóng)具,南方農(nóng)民犁開田地后,仍有大的土塊.農(nóng)人便用六片葉齒組成輥軸,兩側(cè)裝上木板,人跨開兩腳站立,既能掌握平衡,又能增加重量,讓牛拉動輥軸前進(jìn),壓碎土塊,以利于耕種.這六片葉齒又對應(yīng)著菩薩六度,即布施持戒忍辱精進(jìn)禪定與般若.若甲乙每人依次有放回地從這六片葉齒中隨機(jī)取一片,則這兩人選的葉齒對應(yīng)的“度”相同的概率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知平面多邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),現(xiàn)將三角形
的中點(diǎn),現(xiàn)將三角形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
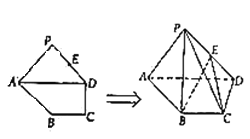
(1)證明:![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠的某種產(chǎn)品成箱包裝,每箱20件,每一箱產(chǎn)品在交付用戶時,用戶要對該箱中部分產(chǎn)品作檢驗(yàn).設(shè)每件產(chǎn)品為不合格品的概率都為![]() ,且各件產(chǎn)品是否合格相互獨(dú)立.
,且各件產(chǎn)品是否合格相互獨(dú)立.
(1)記某一箱20件產(chǎn)品中恰有2件不合格品的概率為![]() ,
,![]() 取最大值時對應(yīng)的產(chǎn)品為不合格品概率為
取最大值時對應(yīng)的產(chǎn)品為不合格品概率為![]() ,求
,求![]() ;
;
(2)現(xiàn)從某一箱產(chǎn)品中抽取3件產(chǎn)品進(jìn)行檢驗(yàn),以(1)中確定的![]() 作為p的值,已知每件產(chǎn)品的檢驗(yàn)費(fèi)用為10元,若檢驗(yàn)出不合格品,則工廠要對每件不合格品支付30元的賠償費(fèi)用,檢驗(yàn)費(fèi)用與賠償費(fèi)用的和記為
作為p的值,已知每件產(chǎn)品的檢驗(yàn)費(fèi)用為10元,若檢驗(yàn)出不合格品,則工廠要對每件不合格品支付30元的賠償費(fèi)用,檢驗(yàn)費(fèi)用與賠償費(fèi)用的和記為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 將
將![]() 的圖象上所有點(diǎn)向左平移
的圖象上所有點(diǎn)向左平移![]() 個單位,然后縱坐標(biāo)不變,橫坐標(biāo)縮短為原來的
個單位,然后縱坐標(biāo)不變,橫坐標(biāo)縮短為原來的![]() ,得到函數(shù)
,得到函數(shù)![]() 的圖象.若
的圖象.若![]() 為偶函數(shù),且最小正周期為
為偶函數(shù),且最小正周期為![]() ,則( )
,則( )
A.![]() 圖象與
圖象與![]() 對稱B.
對稱B.![]() 在
在![]() 單調(diào)遞增
單調(diào)遞增
C.![]() 在
在![]() 有且僅有3個解D.
有且僅有3個解D.![]() 在
在![]() 有僅有3個極大值點(diǎn)
有僅有3個極大值點(diǎn)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知中心在原點(diǎn),焦點(diǎn)在![]() 軸上的橢圓的一個焦點(diǎn)為
軸上的橢圓的一個焦點(diǎn)為![]() ,
,![]() 是橢圓上一點(diǎn).
是橢圓上一點(diǎn).
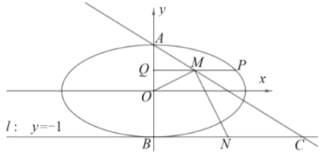
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)設(shè)橢圓的上下頂點(diǎn)分別為![]() ,
,![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]()
![]() 的任意一點(diǎn),
的任意一點(diǎn),![]() 軸,
軸,![]() 為垂足,
為垂足,![]() 為線段
為線段![]() 的中點(diǎn),直線
的中點(diǎn),直線![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 為線段
為線段![]() 的中點(diǎn).
的中點(diǎn).
①求證:![]() ;
;
②若![]() 的面積為
的面積為![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,平面CDEF⊥平面ABCD,且四邊形ABCD為平行四邊形,∠DAB=45°,四邊形CDEF為直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,AD![]() .
.
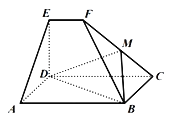
(1)求證:AD⊥BF;
(2)若線段CF上存在一點(diǎn)M,滿足AE∥平面BDM,求![]() 的值;
的值;
(3)若a=1,求二面角D﹣BC﹣F的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,①已知點(diǎn)
中,①已知點(diǎn)![]() ,直線
,直線![]() ,動點(diǎn)P滿足到點(diǎn)Q的距離與到直線
,動點(diǎn)P滿足到點(diǎn)Q的距離與到直線![]() 的距離之比為
的距離之比為![]() .②已知點(diǎn)
.②已知點(diǎn)![]() 是圓
是圓![]() 上一個動點(diǎn),線段HG的垂直平分線交GE于P.③點(diǎn)
上一個動點(diǎn),線段HG的垂直平分線交GE于P.③點(diǎn)![]() 分別在
分別在![]() 軸,y軸上運(yùn)動,且
軸,y軸上運(yùn)動,且![]() ,動點(diǎn)P滿足
,動點(diǎn)P滿足![]() .
.
(1)在①,②,③這三個條件中任選一個,求動點(diǎn)P的軌跡C的方程;
(注:如果選擇多個條件分別解答,按第一個解答計(jì)分)
(2)設(shè)圓![]() 上任意一點(diǎn)A處的切線交軌跡C于M,N兩點(diǎn),試判斷以MN為直徑的圓是否過定點(diǎn)?若過定點(diǎn),求出該定點(diǎn)坐標(biāo).若不過定點(diǎn),請說明理由.
上任意一點(diǎn)A處的切線交軌跡C于M,N兩點(diǎn),試判斷以MN為直徑的圓是否過定點(diǎn)?若過定點(diǎn),求出該定點(diǎn)坐標(biāo).若不過定點(diǎn),請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為坐標(biāo)原點(diǎn),橢圓
為坐標(biāo)原點(diǎn),橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 滿足
滿足![]() .
.
(1)當(dāng)![]() 的傾斜角為
的傾斜角為![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(2)試探究在![]() 軸上是否存在定點(diǎn)
軸上是否存在定點(diǎn)![]() ,使得
,使得![]() 為定值?若存在,求出點(diǎn)
為定值?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com