
【題目】已知函數![]() ,
,![]() ,函數
,函數![]() ,記
,記![]() .把函數
.把函數![]() 的最大值
的最大值![]() 稱為函數
稱為函數![]() 的“線性擬合度”.
的“線性擬合度”.
(1)設函數![]() ,
,![]() ,
,![]() ,求此時函數
,求此時函數![]() 的“線性擬合度”
的“線性擬合度”![]() ;
;
(2)若函數![]() ,
,![]() 的值域為
的值域為![]() (
(![]() ),
),![]() ,求證:
,求證:![]() ;
;
(3)設![]() ,
,![]() ,求
,求![]() 的值,使得函數
的值,使得函數![]() 的“線性擬合度”
的“線性擬合度”![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)證明見解析;(3)當
;(2)證明見解析;(3)當![]() 時,
時,![]() .
.
【解析】
(1)由題意,將![]() 和
和![]() 帶入
帶入![]() 求出
求出![]() 的表達式,求出此時
的表達式,求出此時![]() 的最大值即可;
的最大值即可;
(2)由定義寫出![]() 的表達式,以及
的表達式,以及![]() 可能的取值情況,再用絕對值不等式性質即可得到所求;
可能的取值情況,再用絕對值不等式性質即可得到所求;
(3)寫出![]() 的函數表達式,討論
的函數表達式,討論![]() 的不同取值情況時函數的單調性,求出其對應的
的不同取值情況時函數的單調性,求出其對應的![]() 值.
值.
(1)![]() ,
,
當![]() 時,
時,![]() ,
,
當且僅當![]() ,即
,即![]() 時,取等號,
時,取等號,
所以![]() ,則
,則![]() 在
在![]() 時單調遞減,
時單調遞減,
在![]() 時單調遞增.
時單調遞增.
又![]() ,
,![]() ,所以函數
,所以函數![]() 對于函數
對于函數![]() 的“線性擬合度”
的“線性擬合度”![]() ;
;
(2) 根據定義,![]() ,又
,又![]() ,
,
所以![]() ,
,![]() ,
,
于是![]() .
.
因為![]()
所以![]() ,即
,即![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,
考慮函數![]() ,
,![]() 的值域:
的值域:
① 當![]() 時,
時,![]() 在
在![]() 時單調遞增,
時單調遞增,![]() ,
,
由(2)知,![]() ,
,
當![]() 時,取等號,故
時,取等號,故![]() 最小為
最小為![]() ;
;
② 當![]() 時,
時,![]() ,
,![]() ,
,
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 時單調遞增,
時單調遞增,![]() ,
,
由(2)知,![]() ,
,
當![]() 時,取等號,故
時,取等號,故![]() 最小為
最小為![]() ;;
;;
當![]() ,即
,即![]() 時,
時,![]() ,
,
由(2)知,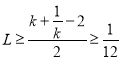 ,當且僅當
,當且僅當![]() 時取等號,
時取等號,![]() 最小為
最小為![]() ;
;
當![]() ,即
,即![]() 時,
時,![]() ,
,
由(2)知,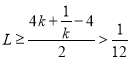 ;
;
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 時單調遞減,
時單調遞減,![]() ,
,
由(2)知,![]() .
.
綜上,當且僅當![]() 時,
時,![]() .
.


 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】下列四個命題中,真命題是( )
A.和兩條異面直線都相交的兩條直線是異面直線
B.和兩條異面直線都相交于不同點的兩條直線是異面直線
C.和兩條異面直線都垂直的直線是異面直線的公垂線
D.若![]() 、
、![]() 是異面直線,
是異面直線,![]() 、
、![]() 是異面直線,則
是異面直線,則![]() 、
、![]() 是異面直線
是異面直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在實數集![]() 上的偶函數
上的偶函數![]() 和奇函數
和奇函數![]() 滿足
滿足![]() .
.
(1)求![]() 與
與![]() 的解析式;
的解析式;
(2)求證:![]() 在區間
在區間![]() 上單調遞增;并求
上單調遞增;并求![]() 在區間
在區間![]() 的反函數;
的反函數;
(3)設![]() (其中
(其中![]() 為常數),若
為常數),若![]() 對于
對于![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某商場2018年洗衣機、電視機和電冰箱三種電器各季度銷量的百分比堆積圖(例如:第3季度內,洗衣機銷量約占![]() ,電視機銷量約占
,電視機銷量約占![]() ,電冰箱銷量約占
,電冰箱銷量約占![]() ).根據該圖,以下結論中一定正確的是( )
).根據該圖,以下結論中一定正確的是( )
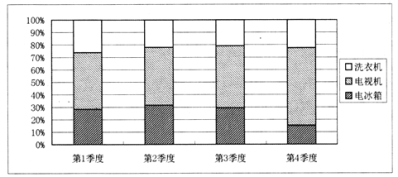
A. 電視機銷量最大的是第4季度
B. 電冰箱銷量最小的是第4季度
C. 電視機的全年銷量最大
D. 電冰箱的全年銷量最大
查看答案和解析>>
科目:高中數學 來源: 題型:
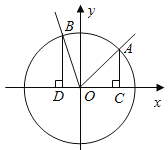
【題目】(本小題滿分13分)如圖,在直角坐標系![]() 中,角
中,角![]() 的頂點是原點,始邊與
的頂點是原點,始邊與![]() 軸正半軸重合.終邊交單位圓于點
軸正半軸重合.終邊交單位圓于點![]() ,且
,且![]() ,將角
,將角![]() 的終邊按逆時針方向旋轉
的終邊按逆時針方向旋轉![]() ,交單位圓于點
,交單位圓于點![]() ,記
,記![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分別過![]() 作
作![]() 軸的垂線,垂足依次為
軸的垂線,垂足依次為![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 數列
數列![]() 滿足
滿足![]() ;數列
;數列![]() 滿足
滿足![]() ;數列
;數列![]() 為公比大于1的等比數列,且
為公比大于1的等比數列,且![]() ,
,![]() 為方程
為方程![]() 的兩個不相等的實根.
的兩個不相等的實根.
(1)求數列![]() 和數列
和數列![]() 的通項公式;
的通項公式;
(2)將數列![]() 中的第
中的第![]() 項,第
項,第![]() 項,第
項,第![]() 項,……,第
項,……,第![]() 項,……刪去后剩余的項按從小到大的順序排成新數列
項,……刪去后剩余的項按從小到大的順序排成新數列![]() ,求數列
,求數列![]() 的前2013項和.
的前2013項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com