Question

【題目】已知橢圓的兩個焦點與短軸的一個頂點構成底邊為，頂角為的等腰三角形．

（1）求橢圓的方程；

（2）設、、是橢圓上三動點，且，線段的中點為，，求的取值范圍．

Answer 1

【答案】（1）（2）

【解析】分析：（1）兩個焦點與短軸的一個頂點構成底邊為，頂角為的等腰三角形．說明，再由直角三角形得，從而可得值，得標準方程；

（2）關鍵是把表示為一個變量的函數，當直線斜率不存在時，可直接求出的長，當直線斜率存在時，設其方程為，與橢圓方程聯立方程組，變形后由判別式寫出一個不等關系，并設，由韋達定理得出，由表示出點坐標代入橢圓方程得，代入剛才的得的關系式：，它滿足判別式＞0，計算中點的坐標，再計算線段長，最終表示為的函數，從而中求得取值范圍．

詳解：（1）由題意，，，∴，

∴橢圓

（2）設，，，

由

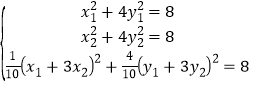∴，得：

當的斜率不存在時，，

由,，得，∴，

當的斜率存在時，設

得：，

，

由點在橢圓上得得：，此時總成立

又，

∴，

∴且，∴且

綜上：