
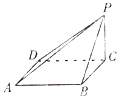
【題目】如圖,四棱錐![]() 中,底面ABCD是正方形,平面
中,底面ABCD是正方形,平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面ABCD.
平面ABCD.
![]() Ⅰ
Ⅰ![]() 證明:
證明:![]() 平面ABCD;
平面ABCD;
![]() Ⅱ
Ⅱ![]() 若二面角
若二面角![]() 的大小為
的大小為![]() ,求PB與平面PAD所成角的大小.
,求PB與平面PAD所成角的大小.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某種植園在芒果臨近成熟時,隨機從一些芒果樹上摘下100個芒果,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經統計得頻率分布直方圖如圖所示.
(單位:克)中,經統計得頻率分布直方圖如圖所示.

(1) 經計算估計這組數據的中位數;
(2)現按分層抽樣從質量為![]() ,
,![]() 的芒果中隨機抽取
的芒果中隨機抽取![]() 個,再從這
個,再從這![]() 個中隨機抽取
個中隨機抽取![]() 個,求這
個,求這![]() 個芒果中恰有
個芒果中恰有![]() 個在
個在![]() 內的概率.
內的概率.
(3)某經銷商來收購芒果,以各組數據的中間數代表這組數據的平均值,用樣本估計總體,該種植園中還未摘下的芒果大約還有![]() 個,經銷商提出如下兩種收購方案:
個,經銷商提出如下兩種收購方案:
A:所以芒果以![]() 元/千克收購;
元/千克收購;
B:對質量低于![]() 克的芒果以
克的芒果以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.
元/個收購.
通過計算確定種植園選擇哪種方案獲利更多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鄉鎮政府為了解決農村教師的住房問題,計劃征用一塊土地蓋一幢建筑總面積為10000![]() 公寓樓(每層的建筑面積相同).已知士地的征用費為
公寓樓(每層的建筑面積相同).已知士地的征用費為![]() ,土地的征用面積為第一層的
,土地的征用面積為第一層的![]() 倍,經工程技術人員核算,第一層建筑費用為
倍,經工程技術人員核算,第一層建筑費用為![]() ,以后每增高一層,其建筑費用就增加
,以后每增高一層,其建筑費用就增加![]() ,設這幢公寓樓高層數為n,總費用為
,設這幢公寓樓高層數為n,總費用為![]() 萬元.(總費用為建筑費用和征地費用之和)
萬元.(總費用為建筑費用和征地費用之和)
(1)若總費用不超過835萬元,求這幢公寓樓最高有多少層數?
(2)試設計這幢公寓的樓層數,使總費用最少,并求出最少費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四邊形![]() 是矩形,
是矩形,![]() ,將
,將![]() 沿著對角線AC翻折,得到
沿著對角線AC翻折,得到![]() ,設頂點
,設頂點![]() 在平面
在平面![]() 上的投影為O.
上的投影為O.
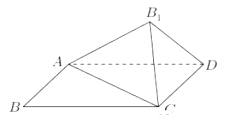
(1)若點O恰好落在邊AD上,①求證:![]() 平面
平面![]() ;②若
;②若![]() ,
,![]() ,當BC取到最小值時,求k的值;
,當BC取到最小值時,求k的值;
(2)當![]() 時,若點O恰好落在
時,若點O恰好落在![]() 的內部(不包括邊界),求二面角
的內部(不包括邊界),求二面角![]() 的余弦值的取值范圍.
的余弦值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個同學家開了一個奶茶店,他為了研究氣溫對熱奶茶銷售杯數的影響,從一季度中隨機選取5天,統計出氣溫與熱奶茶銷售杯數,如表:
氣溫 | 0 | 4 | 12 | 19 | 27 |
熱奶茶銷售杯數 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求熱奶茶銷售杯數關于氣溫的線性回歸方程![]() (
(![]() 精確到0.1),若某天的氣溫為15oC,預測這天熱奶茶的銷售杯數;
精確到0.1),若某天的氣溫為15oC,預測這天熱奶茶的銷售杯數;
(Ⅱ)從表中的5天中任取一天,若已知所選取該天的熱奶茶銷售杯數大于120,求所選取該天熱奶茶銷售杯數大于130的概率.
參考數據:![]() ,
,![]() .參考公式:
.參考公式: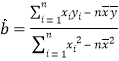 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位員工![]() 人參加“學雷鋒”志愿活動,按年齡分組:第
人參加“學雷鋒”志愿活動,按年齡分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(1)下表是年齡的頻率分布表,求正整數![]() 的值;
的值;
區間 |
|
|
|
|
|
人數 |
|
|
|
|
|
(2)現在要從年齡較小的第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,年齡在第
人,年齡在第![]() 組抽取的員工的人數分別是多少?
組抽取的員工的人數分別是多少?
(3)在(2)的前提下,從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加社區宣傳交流活動,求至少有
人參加社區宣傳交流活動,求至少有![]() 人年齡在第
人年齡在第![]() 組的概率.
組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() 在區間
在區間![]() 上不是單調函數,求實數
上不是單調函數,求實數![]() 的范圍;
的范圍;
(2)若對任意![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設
時,設![]() ,對任意給定的正實數
,對任意給定的正實數![]() ,曲線
,曲線![]() 上是否存在兩點
上是否存在兩點![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 為坐標原點)為直角頂點的直角三角形,而且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,而且此三角形斜邊中點在![]() 軸上?請說明理由.
軸上?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() ,其中
,其中![]() 是自然常數,
是自然常數, ![]() .
.
(1)當![]() 時,求
時,求![]() 的極值,并證明
的極值,并證明![]() 恒成立;
恒成立;
(2)是否存在實數![]() ,使
,使![]() 的最小值為
的最小值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com