
【題目】函數f(x)=x2﹣mx(m>0)在區間[0,2]上的最小值記為g(m)
(1)若0<m≤4,求函數g(m)的解析式;
(2)定義在(﹣∞,0)∪(0,+∞)的函數h(x)為偶函數,且當x>0時,h(x)=g(x),若h(t)>h(4),求實數t的取值范圍.
【答案】
(1)解: f(x)= ![]() .
.
當0<m<4時, ![]() ,∴函數f(x)在
,∴函數f(x)在 ![]() 上時單調遞減,在
上時單調遞減,在 ![]() 上單調遞增.
上單調遞增.
∴當x= ![]() 時,函數f(x)取得最小值,
時,函數f(x)取得最小值, ![]() =﹣
=﹣ ![]() .
.
當m=4時, ![]() =2,函數f(x)在[0,2]內單調遞減,∴當x=
=2,函數f(x)在[0,2]內單調遞減,∴當x= ![]() =2時,函數f(x)取得最小值,
=2時,函數f(x)取得最小值, ![]() =﹣
=﹣ ![]() =﹣1.
=﹣1.
綜上可得:g(m)=﹣ ![]() .
.
(2)解:由題意可得:當x>0時,h(x)=g(x)= ![]() ,∵h(x)是定義在(﹣∞,0)∪(0,+∞)的偶函數,
,∵h(x)是定義在(﹣∞,0)∪(0,+∞)的偶函數,
∴h(x)= ![]() ,x∈(﹣∞,0)∪(0,+∞).
,x∈(﹣∞,0)∪(0,+∞).
∵h(t)>h(4),及h(x)在(0,+∞)上單調遞減,
∴|t|<4,
解得﹣4<t<4,且t≠0.
∴t的取值范圍是(﹣4,0)∪(0,4)
【解析】(1)f(x)= ![]() .由0<m≤4,可得
.由0<m≤4,可得 ![]() ,對m分類討論,利用二次函數的單調性即可得出.(2)由題意可得:當x>0時,h(x)=g(x)=
,對m分類討論,利用二次函數的單調性即可得出.(2)由題意可得:當x>0時,h(x)=g(x)= ![]() ,由于h(x)是定義在(﹣∞,0)∪(0,+∞)的偶函數,可得h(x)=
,由于h(x)是定義在(﹣∞,0)∪(0,+∞)的偶函數,可得h(x)= ![]() ,x∈(﹣∞,0)∪(0,+∞).由于h(t)>h(4),h(x)在(0,+∞)上單調遞減,可得|t|<4,解出即可.
,x∈(﹣∞,0)∪(0,+∞).由于h(t)>h(4),h(x)在(0,+∞)上單調遞減,可得|t|<4,解出即可.
【考點精析】解答此題的關鍵在于理解函數奇偶性的性質的相關知識,掌握在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇,以及對二次函數的性質的理解,了解當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】【2017西安鐵一中五模】已知函數![]() ,其中常數
,其中常數![]() .
.
(Ⅰ)討論![]() 在
在![]() 上的單調性;
上的單調性;
(Ⅱ)當![]() 時,若曲線
時,若曲線![]() 上總存在相異兩點
上總存在相異兩點![]() ,使曲線
,使曲線![]() 在
在![]() 兩點處的切線互相平行,試求
兩點處的切線互相平行,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x,g(x)=ax+2(a>0),且對任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),則實數a的取值范圍是( )
A.[3,+∞)
B.(0,3]
C.[ ![]() ,3]
,3]
D.(0, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一學生共有500人,為了了解學生的歷史學習情況,隨機抽取了50名學生,對他們一年來4次考試的歷史平均成績進行統計,得到頻率分布直方圖如圖所示,后三組頻數成等比數列.
(1)求第五、六組的頻數,補全頻率分布直方圖;
(2)若每組數據用該組區間中點值(例如區間[70,80)的中點值是
75作為代表,試估計該校高一學生歷史成績的平均分;
(3)估計該校高一學生歷史成績在70~100分范圍內的人數.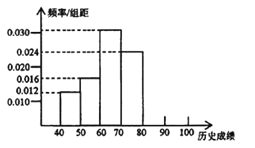
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是奇函數,且在(0,+∞)內是增函數,又f(﹣3)=0,則(x﹣1)f(x)<0的解集是( )
A.{x|﹣3<x<0或1<x<3}
B.{x|1<x<3}
C.{x|x>3或x<﹣3}
D.{x|x<﹣3或x>1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:方程 ![]() =1表示雙曲線,命題q:x∈(0,+∞),x2﹣mx+4≥0恒成立,若p∨q是真命題,且綈(p∧q)也是真命題,求m的取值范圍.
=1表示雙曲線,命題q:x∈(0,+∞),x2﹣mx+4≥0恒成立,若p∨q是真命題,且綈(p∧q)也是真命題,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于圓周率![]() ,數學發展史上出現過許多很有創意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發,我們也可以通過設計下面的實驗來估計
,數學發展史上出現過許多很有創意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發,我們也可以通過設計下面的實驗來估計![]() 的值:先請200名同學,每人隨機寫下一個都小于1的正實數對(x,y);再統計兩數能與1構成鈍角三角形三邊的數對(x,y)的個數m;最后再根據統計數m來估計
的值:先請200名同學,每人隨機寫下一個都小于1的正實數對(x,y);再統計兩數能與1構成鈍角三角形三邊的數對(x,y)的個數m;最后再根據統計數m來估計![]() 的值.假如統計結果是m=56,那么可以估計
的值.假如統計結果是m=56,那么可以估計![]() __________.(用分數表示)
__________.(用分數表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com