
【題目】已知函數(shù)f(x)=asin2x﹣2cos2x+1(a∈R)的圖象經(jīng)過點(﹣![]() ,1)
,1)
(1)求a;
(2)若在區(qū)間[0,m]上存在唯一實數(shù)x0,使得f(x0)=2,求實數(shù)m的取值范圍.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由題意知f(﹣![]() )=1,代值計算求出a;
)=1,代值計算求出a;
(2)由(1)可得f(x)=2sin(2x﹣![]() ),根據(jù)在區(qū)間[0,m]上存在唯一實數(shù)x0,使得f(x0)=2,可得
),根據(jù)在區(qū)間[0,m]上存在唯一實數(shù)x0,使得f(x0)=2,可得![]() ≤2m﹣
≤2m﹣![]() <
<![]() ,解得即可.
,解得即可.
(1)由題意知f(﹣![]() )=1,
)=1,
即asin(﹣![]() )﹣2cos2(﹣
)﹣2cos2(﹣![]() π)+1=1,
π)+1=1,
解得a=![]() ;
;
(2)由(1)可知f(x)=![]() sin2x﹣2cos2x+1=
sin2x﹣2cos2x+1=![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣![]() ),
),
當(dāng)x∈[0,m]時,2x﹣![]() ∈[﹣
∈[﹣![]() ,2m﹣
,2m﹣![]() ],
],
∵在區(qū)間[0,m]上存在唯一實數(shù)x0,使得f(x0)=2,
∴![]() ≤2m﹣
≤2m﹣![]() <
<![]() ,
,
解得![]() ≤m<
≤m<![]() ,
,
故實數(shù)m的取值范圍為[![]() ,
,![]() ).
).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
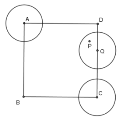
【題目】如圖,邊長為4的正方形![]() 中,半徑為1的動圓Q的圓心Q在邊CD和DA上移動(包含端點A,C,D),P是圓Q上及其內(nèi)部的動點,設(shè),
中,半徑為1的動圓Q的圓心Q在邊CD和DA上移動(包含端點A,C,D),P是圓Q上及其內(nèi)部的動點,設(shè),![]() 則
則![]() 的取值范圍是_____________.
的取值范圍是_____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設(shè)污水凈化管道(管道構(gòu)成Rt△FHE,H是直角項點)來處理污水.管道越長,污水凈化效果越好.設(shè)計要求管道的接口H是AB的中點,E,F(xiàn)分別落在線段BC,AD上.已知AB=20米,AD=![]() 米,記∠BHE=
米,記∠BHE=![]() .
.

(1)試將污水凈化管道的長度L表示為![]() 的函數(shù),并寫出定義域;
的函數(shù),并寫出定義域;
(2)當(dāng)![]() 取何值時,污水凈化效果最好?并求出此時管道的長度L.
取何值時,污水凈化效果最好?并求出此時管道的長度L.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)名著《算法統(tǒng)宗》中有如下問題:“遠(yuǎn)望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數(shù)是上一層燈數(shù)的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 是線段
是線段![]() 上的一點.
上的一點.

(1)若![]() 為
為![]() 的中點,求證:平面
的中點,求證:平面![]() 平面
平面![]() ;
;
(2)當(dāng)點![]() 在什么位置時,
在什么位置時,![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題不正確的是( )
A.研究兩個變量相關(guān)關(guān)系時,相關(guān)系數(shù)r為負(fù)數(shù),說明兩個變量線性負(fù)相關(guān)
B.研究兩個變量相關(guān)關(guān)系時,相關(guān)指數(shù)R2越大,說明回歸方程擬合效果越好.
C.命題“x∈R,cosx≤1”的否定命題為“x0∈R,cosx0>1”
D.實數(shù)a,b,a>b成立的一個充分不必要條件是a3>b3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)設(shè)![]() :實數(shù)x滿足|x﹣m|<2,設(shè)
:實數(shù)x滿足|x﹣m|<2,設(shè)![]() :實數(shù)x滿足
:實數(shù)x滿足![]() >1;若¬p是¬q的必要不充分條件,求實數(shù)m的取值范圍
>1;若¬p是¬q的必要不充分條件,求實數(shù)m的取值范圍
(2)已知p:函數(shù)f(x)=ln(x2﹣ax+3)的定義城為R,已知q:已知![]() 且
且![]() ,指數(shù)函數(shù)g(x)=(a﹣1)x在實數(shù)域內(nèi)為減函數(shù);若¬p∨q為假命題,求實數(shù)a的取值范圍.
,指數(shù)函數(shù)g(x)=(a﹣1)x在實數(shù)域內(nèi)為減函數(shù);若¬p∨q為假命題,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() :
:![]() 關(guān)于直線
關(guān)于直線![]() 對稱且過點
對稱且過點![]() 和
和![]() ,直線
,直線![]() 過定點
過定點![]() .
.
(1)證明:直線![]() 與圓
與圓![]() 相交;
相交;
(2)記直線![]() 與圓
與圓![]() 的兩個交點為
的兩個交點為![]() ,
,![]() .
.
①若弦長![]() ,求直線方程;
,求直線方程;
②求![]() 面積的最大值及
面積的最大值及![]() 面積的最大時的直線方程.
面積的最大時的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
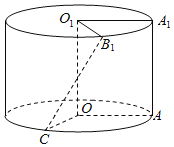
【題目】邊長為1的正方形![]() (及其內(nèi)部)繞的
(及其內(nèi)部)繞的![]() 旋轉(zhuǎn)一周形成圓柱,如圖,
旋轉(zhuǎn)一周形成圓柱,如圖,![]() 長為
長為![]() ,
,![]() 長為
長為![]() ,其中
,其中![]() 與
與![]() 在平面
在平面![]() 的同側(cè).
的同側(cè).
(1)求二面角![]() 的大小;(結(jié)果用反三角函數(shù)值表示)
的大小;(結(jié)果用反三角函數(shù)值表示)
(2)用一平行于![]() 的平面去截這個圓柱,若該截面把圓柱側(cè)面積分成
的平面去截這個圓柱,若該截面把圓柱側(cè)面積分成![]() 兩部分,求
兩部分,求![]() 與該截面的距離;
與該截面的距離;
(3)求線段![]() ,
,![]() 繞著
繞著![]() 旋轉(zhuǎn)
旋轉(zhuǎn)![]() 所形成的幾何體的表面積.
所形成的幾何體的表面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com