
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 是線段
是線段![]() 上的一點.
上的一點.

(1)若![]() 為
為![]() 的中點,求證:平面
的中點,求證:平面![]() 平面
平面![]() ;
;
(2)當點![]() 在什么位置時,
在什么位置時,![]() 平面
平面![]() .
.
【答案】(1)證明見解析;(2)![]() 為靠近
為靠近![]() 點的三等分點.
點的三等分點.
【解析】
(1)連接![]() 、
、![]() ,由中位線的性質(zhì)得出
,由中位線的性質(zhì)得出![]() ,可得出
,可得出![]() 平面
平面![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形,可得出
為平行四邊形,可得出![]() ,進而得出
,進而得出![]() 平面
平面![]() ,再利用面面平行的判定定理可證明出平面
,再利用面面平行的判定定理可證明出平面![]() 平面
平面![]() ;
;
(2)連接![]() 、
、![]() ,設(shè)
,設(shè)![]() ,利用相似三角形得出
,利用相似三角形得出![]() ,由
,由![]() 平面
平面![]() 結(jié)合線面平行的性質(zhì)得出
結(jié)合線面平行的性質(zhì)得出![]() ,再利用平行線分線段成比例定理可確定點
,再利用平行線分線段成比例定理可確定點![]() 的位置.
的位置.
(1)如下圖所示,連接![]() 、
、![]() ,
,
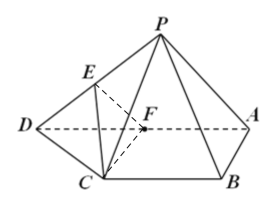
因為![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,所以
的中點,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以,
,所以,![]() 平面
平面![]() ,
,
又因為![]() ,
,![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
又![]() ,所以四邊形
,所以四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)連接![]() 、
、![]() ,設(shè)
,設(shè)![]() ,連接
,連接![]() ,
,
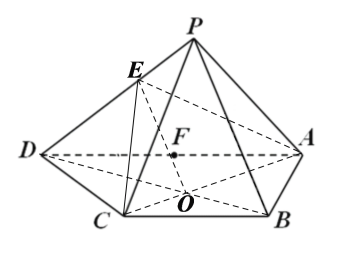
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
![]() ,所以
,所以![]() .
.
在梯形![]() 中,
中,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 為線段
為線段![]() 上靠近
上靠近![]() 點的三等分點.
點的三等分點.


科目:高中數(shù)學 來源: 題型:
【題目】△ABC的內(nèi)角A,B,C的對邊分別為![]() ,已知
,已知![]() 且
且![]() .
.
(1)求角![]() ;
;
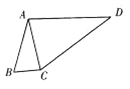
(2)如圖,D為△ABC外一點,若在平面四邊形ABCD中,![]() ,求△ACD面積的最大值.
,求△ACD面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)![]() ,其中,
,其中,![]() 為
為![]() 個互不相同的有限集合,滿足對任意
個互不相同的有限集合,滿足對任意![]() 、
、![]() ,均有
,均有![]() .若
.若![]() (
(![]() 表示有限集合
表示有限集合![]() 的元素個數(shù)),證明:存在
的元素個數(shù)),證明:存在![]() ,使得
,使得![]() 屬于
屬于![]() 中的至少
中的至少![]() 個集合.
個集合.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 、
、![]() 為平面上的兩個定點,且
為平面上的兩個定點,且![]() ,該平面上的動線段
,該平面上的動線段![]() 的端點
的端點![]() 、
、![]() ,滿足
,滿足![]() ,
,![]() ,
,![]() ,則動線段
,則動線段![]() 所形成圖形的面積為( )
所形成圖形的面積為( )
A.36B.60C.72D.108
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=asin2x﹣2cos2x+1(a∈R)的圖象經(jīng)過點(﹣![]() ,1)
,1)
(1)求a;
(2)若在區(qū)間[0,m]上存在唯一實數(shù)x0,使得f(x0)=2,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=ex﹣axlnx.
(1)當a=1時,求曲線f(x)在x=1處的切線方程;
(2)證明:對于a∈(0,e),函數(shù)f(x)在區(qū)間(![]() )上單調(diào)遞增.
)上單調(diào)遞增.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示為一正方體的平面展開圖,在這個正方體中,有下列四個命題:
①AF⊥GC;
②BD與GC成異面直線且夾角為60;
③BD∥MN;
④BG與平面ABCD所成的角為45.
其中正確的個數(shù)是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)生產(chǎn)A、B兩種產(chǎn)品,生產(chǎn)每一噸產(chǎn)品所需的勞動力和煤、電耗如下表:
產(chǎn)品品種 | 勞動力 | 煤 | 電 |
A產(chǎn)品 | 3 | 9 | 4 |
B產(chǎn)品 | 10 | 4 | 5 |
已知生產(chǎn)每噸A產(chǎn)品的利潤是7萬元,生產(chǎn)每噸B產(chǎn)品的利潤是12萬元,現(xiàn)在條件有限,該企業(yè)僅有勞動力300個,煤360噸,并且供電局只能供電200千瓦,試問:該企業(yè)生產(chǎn)A、B兩種產(chǎn)品各多少噸,才能獲得最大利潤?并求出最大利潤.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com