Question

已知函數．

（Ⅰ）當時，求函數的單調增區間；

（Ⅱ）求函數在區間上的最小值．

Answer 1

【命題意圖】本題考查導數的應用，分類討論思想，考查運算求解能力、邏輯思維能力和分析問題解決問題的能力，中等題．

【答案】（Ⅰ）當a＝1時，f(x)＝x²－3x＋lnx，定義域為（0，＋∞）．

f′(x)＝2x－3＋＝＝．

令f′(x)＝0，得x＝1，或x＝．…………………………………………………………………3分

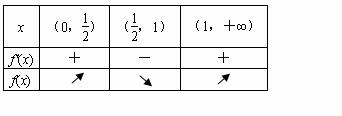
所以函數f(x)的單調增區間為（0，）和（1，＋∞）．…………………………………………6分

（Ⅱ）f′(x)＝2x－(2a＋1)＋＝＝．

令f′(x)＝0，得x＝a，或x＝． …………………………………………………………^……7分

當a≤1時，不論還是，在區間上，均為增函數。

所以[f(x)]_min＝f(1) ＝－2a；…………………………………………………………………………8分

當1＜a＜e時，

所以[f(x)]_min＝f(a) ＝a(lna－a－1)；…………………………………………………………………10分

當a≥e時，

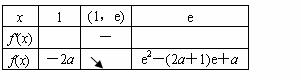
所以[f(x)]_min＝f(e) ＝e²－(2a＋1) e＋a．……………………………………………………………12分

綜上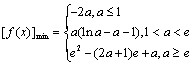，．                                      ……………………………13分