
【題目】某工廠生產某種電子產品,每件產品合格的概率均為![]() ,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗
,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗![]() 件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每
件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次.設該工廠生產
次.設該工廠生產![]() 件該產品,記每件產品的平均檢驗次數為
件該產品,記每件產品的平均檢驗次數為![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)試說明,當![]() 越大時,該方案越合理,即所需平均檢驗次數越少;
越大時,該方案越合理,即所需平均檢驗次數越少;
(ii)當![]() 時,求使該方案最合理時
時,求使該方案最合理時![]() 的值及
的值及![]() 件該產品的平均檢驗次數.
件該產品的平均檢驗次數.
【答案】(1)分布列詳見解析,期望![]() ;(2)(i)詳見解析;(ii)
;(2)(i)詳見解析;(ii)![]() 時平均檢驗次數最少,約
時平均檢驗次數最少,約![]() 次.
次.
【解析】
(1)根據每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次,每件產品的平均檢驗次數
次,每件產品的平均檢驗次數![]() 的可能取值為
的可能取值為![]() ,
,![]() ,再利用獨立事件和互斥事件求得概率列出分布列,再求期望
,再利用獨立事件和互斥事件求得概率列出分布列,再求期望
(2)(i)由(1)知![]() ,根據指數函數的單調性得到
,根據指數函數的單調性得到![]() 在
在![]() 上單調遞減,從而得到結論. (ii)由(1)記
上單調遞減,從而得到結論. (ii)由(1)記![]() ,則由
,則由![]() 且取最小值時,該方案最合理求解.
且取最小值時,該方案最合理求解.
(1)由題意,![]() 的可能取值為
的可能取值為![]() ,
,![]()
![]() ,
,![]() ,
,
故![]() 的分布列為
的分布列為
|
|
|
|
|
|
![]()
(2)(i)由(1),記![]() ,
,
因為![]() .所以
.所以![]() 在
在![]() 上單調遞減,
上單調遞減,
故![]() 越大,
越大,![]() 越小,即所需平均檢驗次數越少,該方案越合理.
越小,即所需平均檢驗次數越少,該方案越合理.
(ii)記![]() ,當
,當![]() 且取最小值時,該方案最合理,
且取最小值時,該方案最合理,
因為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 時平均檢驗次數最少,約
時平均檢驗次數最少,約![]() 次.
次.


科目:高中數學 來源: 題型:
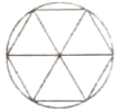
【題目】劉徽(約公元225年—295年),魏晉期間偉大的數學家,中國古典數學理論的奠基人之一.他在割圓術中提出的“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體,而無所失矣”.這可視為中國古代極限觀念的佳作.割圓術的核心思想是將一個圓的內接正![]() 邊形等分成
邊形等分成![]() 個等腰三角形(如圖所示),當
個等腰三角形(如圖所示),當![]() 變得很大時,這
變得很大時,這![]() 個等腰三角形的面積之和近似等于圓的面積.運用割圓術的思想,估計
個等腰三角形的面積之和近似等于圓的面積.運用割圓術的思想,估計![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以原點O為極點,以x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
中,以原點O為極點,以x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (t為參數),
(t為參數),![]() ,點A為直線
,點A為直線![]() 與曲線C在第二象限的交點,過O點的直線
與曲線C在第二象限的交點,過O點的直線![]() 與直線
與直線![]() 互相垂直,點B為直線
互相垂直,點B為直線![]() 與曲線C在第三象限的交點.
與曲線C在第三象限的交點.
(1)寫出曲線C的直角坐標方程及直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在郊野公園的景觀河的兩岸,![]() 、
、![]() 是夾角為120°的兩條岸邊步道(長度均超過
是夾角為120°的兩條岸邊步道(長度均超過![]() 千米),為方便市民觀光游覽,現準備在河道拐角處的另一側建造一個觀景臺
千米),為方便市民觀光游覽,現準備在河道拐角處的另一側建造一個觀景臺![]() ,在兩條步道
,在兩條步道![]() 、
、![]() 上分別設立游客上下點
上分別設立游客上下點![]() 、
、![]() ,從
,從![]() 、
、![]() 到觀景臺
到觀景臺![]() 建造兩條游船觀光線路
建造兩條游船觀光線路![]() 、
、![]() ,測得
,測得![]() 千米.
千米.
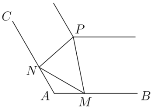
(1)求游客上下點![]() 、
、![]() 間的距離;
間的距離;
(2)若![]() ,設
,設![]() ,求兩條觀光線路
,求兩條觀光線路![]() 與
與![]() 之和關于
之和關于![]() 的表達式
的表達式![]() ,并求其最大值.
,并求其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了提高生產線的運行效率,工廠對生產線的設備進行了技術改造.為了對比技術改造后的效果,采集了生產線的技術改造前后各20次連續正常運行的時間長度(單位:天)數據,并繪制了如莖葉圖:
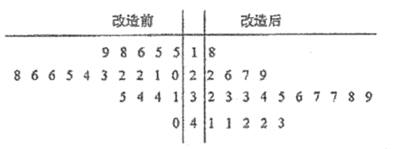
(1)(i)設所采集的40個連續正常運行時間的中位數m,并將連續正常運行時間超過m和不超過m的次數填入下面的列聯表:
超過 | 不超過 | |
改造前 | ||
改造后 |
(ii)根據(i)中的列聯表,能否有99%的把握認為生產線技術改造前后的連續正常運行時間有差異?
附: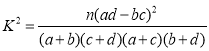
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)工廠的生產線的運行需要進行維護,工廠對生產線的生產維護費用包括正常維護費、保障維護費兩種.對生產線設定維護周期為T天(即從開工運行到第kT天![]() 進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元/次;保障維護費第一次為0.2萬元/周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:
進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元/次;保障維護費第一次為0.2萬元/周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:![]() ,
,![]() .以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列.
.以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
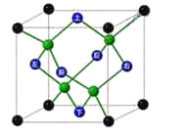
【題目】金剛石是碳原子的一種結構晶體,屬于面心立方晶胞(晶胞是構成晶體的最基本的幾何單元),即碳原子處在立方體的![]() 個頂點,
個頂點,![]() 個面的中心,此外在立方體的對角線的
個面的中心,此外在立方體的對角線的![]() 處也有
處也有![]() 個碳原子,如圖所示(綠色球),碳原子都以共價鍵結合,原子排列的基本規律是每一個碳原子的周圍都有
個碳原子,如圖所示(綠色球),碳原子都以共價鍵結合,原子排列的基本規律是每一個碳原子的周圍都有![]() 個按照正四面體分布的碳原子.設金剛石晶胞的棱長為
個按照正四面體分布的碳原子.設金剛石晶胞的棱長為![]() ,則正四面體
,則正四面體![]() 的棱長為__________;正四面體
的棱長為__________;正四面體![]() 的外接球的體積是__________.
的外接球的體積是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com