
【題目】設函數![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,
,![]() ,求函數在
,求函數在![]() 處的切線方程;
處的切線方程;
(2)討論![]() 的單調區間.
的單調區間.
【答案】(1)![]() ;(2)a>0時,f(x)的增區間為(﹣∞,
;(2)a>0時,f(x)的增區間為(﹣∞,![]() ),(
),(![]() ,+∞),減區間為(
,+∞),減區間為(![]() ,
,![]() );a≤0時,f(x)的單調遞增區間為(﹣∞,+∞),無減區間.
);a≤0時,f(x)的單調遞增區間為(﹣∞,+∞),無減區間.
【解析】
(1)當a=1,b=2時,可得f(x),f′(x),而切線斜率k=f′(1),易求f(1),從而可得切點坐標,由點斜式可得切線方程;
(2)求出f(x)的導數,討論a≤0時f′(x)≥0,f(x)在R上遞增;當a>0時,由導數大于0,可得增區間;導數小于0,可得減區間;
(1)當a=1,b=2時,f(x)=x3﹣x-2,f′(x)=3x2﹣1,
則切線斜率k=f′(1)=2,
f(1)=1﹣1-2=-2,則切點為(1,-2),
∴函數f(x)在(1,f(1))處的切線方程為y+2=2(x﹣1),即y=2x-4;
(2)若f(x)=x3﹣ax﹣b,則f′(x)=3x2﹣a,
分兩種情況討論:
①當a≤0時,有f′(x)=3x2﹣a≥0恒成立,
此時f(x)的單調遞增區間為(﹣∞,+∞),無減區間.
②當a>0時,令f′(x)=3x2﹣a=0,解得x![]() 或x
或x![]() ,
,
當x![]() 或x
或x![]() 時,f′(x)=3x2﹣a>0,f(x)為增函數,
時,f′(x)=3x2﹣a>0,f(x)為增函數,
當![]() x
x![]() 時,f′(x)=3x2﹣a<0,f(x)為減函數,
時,f′(x)=3x2﹣a<0,f(x)為減函數,
故f(x)的增區間為(﹣∞,![]() ),(
),(![]() ,+∞),減區間為(
,+∞),減區間為(![]() ,
,![]() );
);


科目:高中數學 來源: 題型:
【題目】大連市某企業為確定下一年投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位:![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根據散點圖判斷,
![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
![]() 根據
根據![]() 的判斷結果及表中數據,建立
的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
![]() 已知這種產品的年利潤
已知這種產品的年利潤![]() 與
與![]() 、
、![]() 的關系為
的關系為![]() .根據
.根據![]() 的結果回答下列問題:
的結果回答下列問題:
![]() 年宣傳費
年宣傳費![]() 時,年銷售量及年利潤的預報值是多少?
時,年銷售量及年利潤的預報值是多少?
![]() 年宣傳費
年宣傳費![]() 為何值時,年利潤的預報值最大?
為何值時,年利潤的預報值最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
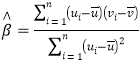 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點
的焦點![]() 重合,且橢圓短軸的兩個端點與點
重合,且橢圓短軸的兩個端點與點![]() 構成正三角形.
構成正三角形.
(1)求橢圓的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,試問在
,試問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使
,使![]() 恒為定值?若存在,求出
恒為定值?若存在,求出![]() 的坐標,并求出這個定值;若不存在,請說明理由.
的坐標,并求出這個定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 與
與![]() 的圖象關于
的圖象關于![]() 軸對稱,當函數
軸對稱,當函數![]() 和
和![]() 在區間
在區間![]() 同時遞增或同時遞減時,把區間
同時遞增或同時遞減時,把區間![]() 叫做函數
叫做函數![]() 的“不動區間”.若區間
的“不動區間”.若區間![]() 為函數
為函數![]() 的“不動區間”,則實數
的“不動區間”,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面四邊形ABCD中,已知A=![]() ,B=
,B=![]() ,AB=6.在AB邊上取點E,使得BE=1,連接EC,ED.若∠CED=
,AB=6.在AB邊上取點E,使得BE=1,連接EC,ED.若∠CED=![]() ,EC=
,EC=![]() .
.

(1)求sin∠BCE的值;
(2)求CD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg),其頻率分布直方圖如下:

(1)根據箱產量的頻率分布直方圖填寫下面![]() 列聯表,從等高條形圖中判斷箱產量是否與新、舊網箱養殖方法有關;
列聯表,從等高條形圖中判斷箱產量是否與新、舊網箱養殖方法有關;
(2)根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關?
箱產量<50kg | 箱產量≥50kg | |
舊養殖法 | ||
新養殖法 |
參考公式:
(1)給定臨界值表
P(K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)![]() 其中
其中![]() 為樣本容量.
為樣本容量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com