
【題目】求函數y= ![]() 的值域.
的值域.
【答案】解:方法一: y= ![]() =
= ![]() =3﹣
=3﹣ ![]() ,
,
∵x2+2≥2,
∴0< ![]() ≤
≤ ![]() ,
,
0< ![]() ≤
≤ ![]() ,﹣
,﹣ ![]() ≤﹣
≤﹣ ![]() <0,
<0,
3﹣ ![]() ≤3﹣
≤3﹣ ![]() <3,
<3,
即 ![]() ≤y<3,
≤y<3,
即函數的值域為[ ![]() ,3).
,3).
方法二:
由y= ![]() 得yx2+2y=3x2﹣1,
得yx2+2y=3x2﹣1,
即(3﹣y)x2=2y+1,
當y=3時,方程等價為0=7,不成立,
則y≠3,
∴x2= ![]() ≥0,
≥0,
得 ![]() ≤y<3,
≤y<3,
即函數的值域為[ ![]() ,3)
,3)
【解析】利用分式函數的性質以及轉化法進行求解即可.
【考點精析】本題主要考查了函數的值域的相關知識點,需要掌握求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的才能正確解答此題.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)= ![]() 滿足f(0)=0.
滿足f(0)=0.
(1)求a,f(﹣2)的值,判斷函數f(x)的奇偶性并說明理由;
(2)判斷該函數在R上的單調性(不要求證明),解不等式f(x2+x)< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱柱ABC﹣A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是邊長為2的等邊三角形,AA′=3,E、F分別在棱AA′,CC′上,且AE=C′F=2. 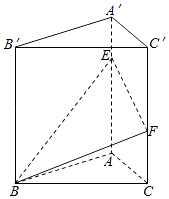
(1)求證:BB′⊥底面ABC;
(2)在棱A′B′上是否存在一點M,使得C′M∥平面BEF,若存在,求 ![]() 值,若不存在,說明理由;
值,若不存在,說明理由;
(3)求棱錐A′﹣BEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市準備在道路EF的一側修建一條運動比賽道,賽道的前一部分為曲線段FBC,該曲線段是函數 ![]() (A>0,ω>0),x∈[﹣4,0]時的圖象,且圖象的最高點為B(﹣1,2).賽道的中間部分為長
(A>0,ω>0),x∈[﹣4,0]時的圖象,且圖象的最高點為B(﹣1,2).賽道的中間部分為長 ![]() 千米的直線跑道CD,且CD∥EF.賽道的后一部分是以O為圓心的一段圓弧
千米的直線跑道CD,且CD∥EF.賽道的后一部分是以O為圓心的一段圓弧 ![]() .
. 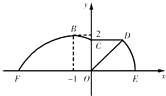
(1)求ω的值和∠DOE的大小;
(2)若要在圓弧賽道所對應的扇形ODE區域內建一個“矩形草坪”,矩形的一邊在道路EF上,一個頂點在半徑OD上,另外一個頂點P在圓弧 ![]() 上,且∠POE=θ,求當“矩形草坪”的面積取最大值時θ的值.
上,且∠POE=θ,求當“矩形草坪”的面積取最大值時θ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線l1:y=x,l2:y=x+2與圓C:x2+y2﹣2mx﹣2ny=0的四個交點把圓C分成的四條弧長相等,則m=( )
A.0或1
B.0或﹣1
C.1或﹣1
D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosλθ,cos(10﹣λ)θ),
=(cosλθ,cos(10﹣λ)θ), ![]() =(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
=(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]() ⊥
⊥ ![]() ,求θ;
,求θ;
(3)若θ= ![]() ,求證:
,求證: ![]() ∥
∥ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() ,
, ![]() .
.
(1)當n=1,2,3時,分別比較f(n)與g(n)的大小(直接給出結論);
(2)由(1)猜想f(n)與g(n)的大小關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數f(x)=4sin(2x ![]() )(x∈R),有下列命題: ①y=f(x)的表達式可改寫為y=4cos(2x﹣
)(x∈R),有下列命題: ①y=f(x)的表達式可改寫為y=4cos(2x﹣ ![]() );
);
②y=f(x)是以2π為最小正周期的周期函數;
③y=f(x)的圖象關于點 ![]() 對稱;
對稱;
④y=f(x)的圖象關于直線x=﹣ ![]() 對稱.
對稱.
其中正確的命題的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com