
【題目】已知不等式|x+3|﹣2x﹣1<0的解集為(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函數(shù)f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零點(diǎn),求實數(shù)m的值.
|﹣x0(m>0)有零點(diǎn),求實數(shù)m的值.
【答案】解:(Ⅰ)不等式轉(zhuǎn)化為 ![]() 或
或 ![]() ,
,
解得x>2,∴x0=2;
(Ⅱ)由題意,等價于|x﹣m|+|x+ ![]() |=2(m>0)有解,
|=2(m>0)有解,
∵|x﹣m|+|x+ ![]() |≥m+
|≥m+ ![]() ,當(dāng)且僅當(dāng)(x﹣m)(x+
,當(dāng)且僅當(dāng)(x﹣m)(x+ ![]() )≤0時取等號,
)≤0時取等號,
∵|x﹣m|+|x+ ![]() |=2(m>0)有解,
|=2(m>0)有解,
∴m+ ![]() ≤2,
≤2,
∵m+ ![]() ≥2,
≥2,
∴m+ ![]() =2,∴m=1
=2,∴m=1
【解析】(Ⅰ)不等式轉(zhuǎn)化為 ![]() 或
或 ![]() ,解得x>2,即可求x0的值;(Ⅱ)由題意,等價于|x﹣m|+|x+
,解得x>2,即可求x0的值;(Ⅱ)由題意,等價于|x﹣m|+|x+ ![]() |=2(m>0)有解,結(jié)合基本不等式,即可求實數(shù)m的值.
|=2(m>0)有解,結(jié)合基本不等式,即可求實數(shù)m的值.
【考點(diǎn)精析】關(guān)于本題考查的絕對值不等式的解法,需要了解含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對值的符號才能得出正確答案.


 計算高手系列答案
計算高手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知(x+ ![]() )n展開式的二項式系數(shù)之和為256
)n展開式的二項式系數(shù)之和為256
(1)求n;
(2)若展開式中常數(shù)項為 ![]() ,求m的值;
,求m的值;
(3)若展開式中系數(shù)最大項只有第6項和第7項,求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為 ![]() ,
, ![]() ,點(diǎn)
,點(diǎn) ![]() 在橢圓上,
在橢圓上, ![]() ,且
,且 ![]() 的面積為4.
的面積為4.
(1)求橢圓的方程;
(2)點(diǎn) ![]() 是橢圓上任意一點(diǎn),
是橢圓上任意一點(diǎn), ![]() 分別是橢圓的左、右頂點(diǎn),直線
分別是橢圓的左、右頂點(diǎn),直線 ![]() 與直線
與直線 ![]() 分別交于
分別交于 ![]() 兩點(diǎn),試證:以
兩點(diǎn),試證:以 ![]() 為直徑的圓交
為直徑的圓交 ![]() 軸于定點(diǎn),并求該定點(diǎn)的坐標(biāo).
軸于定點(diǎn),并求該定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,設(shè)橢圓 ![]() =1(a>b>0)的左、右焦點(diǎn)分別為F1 , F2 , 右頂點(diǎn)為A,上頂點(diǎn)為B,離心率為e.橢圓上一點(diǎn)C滿足:C在x軸上方,且CF1⊥x軸.
=1(a>b>0)的左、右焦點(diǎn)分別為F1 , F2 , 右頂點(diǎn)為A,上頂點(diǎn)為B,離心率為e.橢圓上一點(diǎn)C滿足:C在x軸上方,且CF1⊥x軸.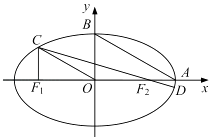
(1)若OC∥AB,求e的值;
(2)連結(jié)CF2并延長交橢圓于另一點(diǎn)D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() 展開式各項系數(shù)的和比它的二項式系數(shù)的和大992.
展開式各項系數(shù)的和比它的二項式系數(shù)的和大992.
(Ⅰ)求n;
(Ⅱ)求展開式中 ![]() 的項;
的項;
(Ⅲ)求展開式系數(shù)最大項.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】美索不達(dá)米亞平原是人類文明的發(fā)祥地之一.美索不達(dá)米亞人善于計算,他們創(chuàng)造了優(yōu)良的計數(shù)系統(tǒng),其中開平方算法是最具有代表性的.程序框圖如圖所示,若輸入a,n,ξ的值分別為8,2,0.5,(每次運(yùn)算都精確到小數(shù)點(diǎn)后兩位)則輸出結(jié)果為( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知半徑為1的球O內(nèi)切于正四面體A﹣BCD,線段MN是球O的一條動直徑(M,N是直徑的兩端點(diǎn)),點(diǎn)P是正四面體A﹣BCD的表面上的一個動點(diǎn),則 ![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù) ![]() 是奇函數(shù)
是奇函數(shù) ![]() (
( ![]() )的導(dǎo)函數(shù),
)的導(dǎo)函數(shù), ![]() ,當(dāng)
,當(dāng) ![]() 時,
時, ![]() 則使得
則使得 ![]() 成立的
成立的 ![]() 的取值范圍是( )
的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】命題 ![]() :關(guān)于
:關(guān)于 ![]() 的不等式
的不等式 ![]() 對一切
對一切 ![]() 恒成立,命題
恒成立,命題 ![]() :指數(shù)函數(shù)
:指數(shù)函數(shù) ![]() 是增函數(shù),若
是增函數(shù),若 ![]() 或
或 ![]() 為真、
為真、 ![]() 且
且 ![]() 為假,求實數(shù)
為假,求實數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com