
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若關于![]() 的不等式
的不等式![]() 恒成立,求整數
恒成立,求整數![]() 的最小值.
的最小值.
【答案】(1) 當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為![]() ,無減區間,
,無減區間,
當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為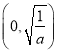 ,單調遞減區間為
,單調遞減區間為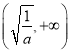 ;(2)2.
;(2)2.
【解析】試題分析:
(1)首先對函數求導,然后對參數分類討論可得當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為![]() ,無減區間,
,無減區間,
當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為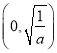 ,單調遞減區間為
,單調遞減區間為 ;
;
(2)將原問題轉化為![]() 在
在![]() 上恒成立,考查函數
上恒成立,考查函數![]() 的性質可得整數
的性質可得整數![]() 的最小值是2.
的最小值是2.
試題解析:
(1) ![]() ,函數
,函數![]() 的定義域為
的定義域為![]() .
.
當![]() 時,
時, ![]() ,則
,則![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,令
時,令![]() ,則
,則![]() 或
或![]() (舍負),
(舍負),
當![]() 時,
時, ![]() ,
, ![]() 為增函數,
為增函數,
當![]() 時,
時, ![]() ,
, ![]() 為減函數,
為減函數,
∴當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為![]() ,無減區間,
,無減區間,
當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為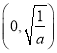 ,單調遞減區間為
,單調遞減區間為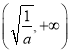 .
.
(2)解法一:由![]() 得
得![]() ,
,
∵![]() ,
,
∴原命題等價于![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
則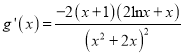 ,
,
令![]() ,則
,則![]() 在
在![]() 上單調遞增,
上單調遞增,
由![]() ,
, ![]() ,
,
∴存在唯一![]() ,使
,使![]() ,
, ![]() .
.
∴當![]() 時,
時, ![]() ,
, ![]() 為增函數,
為增函數,
當![]() 時,
時, ![]() ,
, ![]() 為減函數,
為減函數,
∴![]() 時,
時, ![]() ,
,
∴![]() ,
,
又![]() ,則
,則![]() ,
,
由![]() ,所以
,所以![]() .
.
故整數![]() 的最小值為2.
的最小值為2.
解法二: ![]() 得,
得,
![]() ,
,
令![]() ,
,
![]() ,
,
①![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調遞減,
上單調遞減,
∵![]() ,∴該情況不成立.
,∴該情況不成立.
②![]() 時,
時, ![]()
當![]() 時,
時, ![]() ,
, ![]() 單調遞減;
單調遞減;
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
∴![]() ,
,
![]() 恒成立
恒成立![]() ,
,
即![]() .
.
令![]() ,顯然
,顯然![]() 為單調遞減函數.
為單調遞減函數.
由![]() ,且
,且![]() ,
, ![]() ,
,
∴當![]() 時,恒有
時,恒有![]() 成立,
成立,
故整數![]() 的最小值為2.
的最小值為2.
綜合①②可得,整數![]() 的最小值為2.
的最小值為2.


科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,在以極點為直角坐標原點
,在以極點為直角坐標原點![]() ,極軸為
,極軸為![]() 軸的正半軸建立的平面直角坐標系
軸的正半軸建立的平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為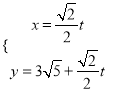 (
(![]() 為參數).
為參數).
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)在平面直角坐標系中,設曲線![]() 經過伸縮變換
經過伸縮變換![]() :
:  得到曲線
得到曲線![]() ,若
,若![]() 為曲線
為曲線![]() 上任意一點,求點
上任意一點,求點![]() 到直線
到直線![]() 的最小距離.
的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在探究實系數一元二次方程的根與系數的關系時,可按下述方法進行:
設實系數一元二次方程![]() ……①
……①
在復數集![]() 內的根為
內的根為![]() ,
, ![]() ,則方程①可變形為
,則方程①可變形為![]() ,
,
展開得![]() .……②
.……②
比較①②可以得到: 
類比上述方法,設實系數一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在復數集
)在復數集![]() 內的根為
內的根為![]() ,
, ![]() ,…,
,…, ![]() ,則這
,則這![]() 個根的積
個根的積![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次反恐演習中,我方三架武裝直升機分別從不同方位對同一目標發動攻擊(各發射一枚導彈),由于天氣原因,三枚導彈命中目標的概率分別為0.9,0.9,0.8,若至少有兩枚導彈命中目標方可將其摧毀,則目標被摧毀的概率為( )
A. 0.998 B. 0.046 C. 0.002 D. 0.954
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在其定義域內為增函數,求
在其定義域內為增函數,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,設函數![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com