
���}Ŀ�������������}�ķ����Д��������}����٣�
��1��![]() ��
��
��2���е��������ǵ�߅�����Σ�
��3����һ��(g��)ż��(sh��)����?c��i)?sh��)
��4������ɂ�(g��)��߅�����ζ����ƣ�
��5��![]() ��
��
���𰸡���1��![]() �������}��
�������}��
��2�����е������ζ����ǵ�߅�����Σ������}��
��3������һ��(g��)ż��(sh��)��������?c��i)?sh��)�������}��
��4�����ڃɂ�(g��)��߅�����β����ƣ������}��
��5��![]() �������}��
�������}��
��������
����(j��)ȫ�Q���}�ķ��طQ���}���طQ���}�ķ�ȫ�Q���}������������Д������.
�⣺��1��![]()
![]() �����طQ���}��
�����طQ���}��
������飺![]() ��
��![]() .
.
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �����Ǽ����}��
�����Ǽ����}��
��2��![]() �е��������ǵ�߅�����Σ����طQ���},
�е��������ǵ�߅�����Σ����طQ���},
������飺���е������ζ��ǵ�߅�����Σ��@Ȼ�Ǽ����}��
��3��![]() ����һ��(g��)ż��(sh��)����?c��i)?sh��)�����طQ���}��
����һ��(g��)ż��(sh��)����?c��i)?sh��)�����طQ���}��
������飺����ż��(sh��)��������?c��i)?sh��).
��?y��n)?/span>![]() ��ż��(sh��)��������?c��i)?sh��)�����Ǽ����}��
��ż��(sh��)��������?c��i)?sh��)�����Ǽ����}��
��4��![]() ������ɂ�(g��)��߅�����ζ����ơ�����ȫ�Q���}��
������ɂ�(g��)��߅�����ζ����ơ�����ȫ�Q���}��
������飺��Щ��߅�����β�����.
��?y��n)������߅������������(g��)�Ƕ���ȣ�����![]() ��������ɂ�(g��)��߅���Ƕ����ƣ��������}��
��������ɂ�(g��)��߅���Ƕ����ƣ��������}��
�����}����Щ��߅�����β�����.���Ǽ����}.
��5��![]()
![]() �����طQ���}��
�����طQ���}��
������飺![]()
![]() ��
��
![]() ����
����![]() �o(w��)��(sh��)��(sh��)��������(du��)���⌍(sh��)��(sh��)
�o(w��)��(sh��)��(sh��)��������(du��)���⌍(sh��)��(sh��)![]() ���������������}.
���������������}.


 �W(xu��)����(y��u)㕽ӽ̲��Ͼ���W(xu��)������ϵ�д�
�W(xu��)����(y��u)㕽ӽ̲��Ͼ���W(xu��)������ϵ�д� С�W(xu��)�n�����I(y��)ϵ�д�
С�W(xu��)�n�����I(y��)ϵ�д� ��ʿһ�c(di��n)ȫͨϵ�д�
��ʿһ�c(di��n)ȫͨϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�A![]() �͒��タ
�͒��タ![]() ���A
���A![]() �c���タ
�c���タ![]() �Ĝ�(zh��n)������
�Ĝ�(zh��n)������![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ����e��
����e��![]() ������
������![]() ��
��![]() �Ľ��c(di��n).
�Ľ��c(di��n).
��1�����タ![]() �ķ��̣�
�ķ��̣�
��2�����^ԭ�c(di��n)![]() �Ą�(d��ng)ֱ��
�Ą�(d��ng)ֱ��![]() ��ԓ���タ��
��ԓ���タ��![]() ��
��![]() ���c(di��n)���ҝM��
���c(di��n)���ҝM��![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ��A
��A![]() ������һ��(d��ng)�c(di��n)����(d��ng)��(d��ng)�c(di��n)
������һ��(d��ng)�c(di��n)����(d��ng)��(d��ng)�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x���r(sh��)ֱ��
�ľ��x���r(sh��)ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���b�S���a(ch��n)һ�N���b��ÿ�����b�ijɱ���40Ԫ�����S�r(ji��)��60Ԫ��ԓ�S��Ą�(l��)�N����ӆُ(g��u)���Q����(d��ng)һ��ӆُ(g��u)�����^100���r(sh��)��ÿ��ӆُ(g��u)һ����ӆُ(g��u)��ȫ�����b�ij��S�r(ji��)�ͽ���0.02Ԫ������(j��)�Ј�(ch��ng)�{(di��o)�飬�N����һ��ӆُ(g��u)������(hu��)���^500��.
��1���O(sh��)һ��ӆُ(g��u)����x�������b�Č�(sh��)�H���S�r(ji��)��PԪ����������(sh��)![]() �ı��_(d��)ʽ��
�ı��_(d��)ʽ��
��2����(d��ng)�N����һ��ӆُ(g��u)450�����b�r(sh��)��ԓ���b�S�@�õ�����(r��n)�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ���溯��(sh��)����
���溯��(sh��)����![]() ������
������![]() ��
��![]() .
.
��1����![]() ��
��![]() ��ֵ.
��ֵ.
��2����![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-5������ʽ�x�v
�O(sh��)����(sh��)![]() .
.
������![]() ����Сֵ��ȡ����Сֵ�r(sh��)
����Сֵ��ȡ����Сֵ�r(sh��)![]() ��ȡֵ������
��ȡֵ������
����������![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ĈD�����c(di��n)
�ĈD�����c(di��n)![]() ̎���о���
̎���о���![]() ����
����![]() Ҳ�麯��(sh��)
Ҳ�麯��(sh��)![]() �ĈD����о����t
�ĈD����о����t![]() ��횝M���� ��
��횝M���� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������������}�ķ�,���Д�����٣�
��1���κ����픵(sh��)���nj�(sh��)��(sh��)��
��2������һ��(g��)��(sh��)��(sh��)![]() ����ʹ
����ʹ![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����5cm���λ�L(zh��ng)������λ�A,�քe����![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() �ǵ����Ҿ����Ҿ������о�,�����������L(zh��ng)��,�����@Щ�ǵ��������Һ����еĽ���ֵ,��ʹ�ÿƌW(xu��)Ӌ(j��)�������@Щ�ǵ��������Һ�����,���M(j��n)�б��^.
�ǵ����Ҿ����Ҿ������о�,�����������L(zh��ng)��,�����@Щ�ǵ��������Һ����еĽ���ֵ,��ʹ�ÿƌW(xu��)Ӌ(j��)�������@Щ�ǵ��������Һ�����,���M(j��n)�б��^.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���քe�^�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() �Ą�(d��ng)ֱ��
�Ą�(d��ng)ֱ��![]() �ཻ��
�ཻ��![]() �c(di��n)���c�E�A
�c(di��n)���c�E�A![]() �քe����
�քe����![]() �c
�c![]() ��ͬ���c(di��n)��ֱ��
��ͬ���c(di��n)��ֱ��![]() ��б��
���![]() �M��
�M��![]() ����֪��(d��ng)
����֪��(d��ng)![]() �c
�c![]() �S�غϕr(sh��)��
�S�غϕr(sh��)��![]() ��
��![]() .
.
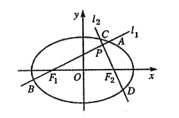
������E�A![]() �ķ��̣�
�ķ��̣�
�����Ƿ���ڶ��c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ�������ڣ����
�鶨ֵ�������ڣ����![]() �c(di��n)����(bi��o)������˶�ֵ���������ڣ��f�����ɣ�
�c(di��n)����(bi��o)������˶�ֵ���������ڣ��f�����ɣ�
���𰸡�����![]() ��������
��������![]() ��
��![]() ��
��![]() .
.
��������ԇ�}��������1����(d��ng)![]() �c
�c![]() �S�غϕr(sh��)��
�S�غϕr(sh��)��![]() ��ֱ��
��ֱ��![]() �S����
�S����![]() ,��
,��![]() ,
,![]() �Ķ��ÙE�A�ķ��̣���2�����}Ŀ���������ɶ��c(di��n)���t
�Ķ��ÙE�A�ķ��̣���2�����}Ŀ���������ɶ��c(di��n)���t![]() �c(di��n)��܉�E�ǙE�A�����p���� ������
�c(di��n)��܉�E�ǙE�A�����p���� ������![]() ����(bi��o)�����ɵ�
����(bi��o)�����ɵ�![]() �c(di��n)��܉�E�ǙE�A���Ķ���ö��c(di��n)
�c(di��n)��܉�E�ǙE�A���Ķ���ö��c(di��n)![]() ���c(di��n)
���c(di��n)![]() .
.
ԇ�}������![]() ��(d��ng)
��(d��ng)![]() �c
�c![]() �S�غϕr(sh��)��
�S�غϕr(sh��)��![]() , ��
, ��![]() ,����
,����![]() ��ֱ��
��ֱ��![]() �S����
�S����![]() ��
��![]() ��, ��
��, ��![]() ,
,![]() �E�A
�E�A![]() �ķ��̞�
�ķ��̞�![]() .
.
![]() ���c(di��n)
���c(di��n)![]() ����(bi��o)�քe��
����(bi��o)�քe��![]() , ��(d��ng)ֱ��
, ��(d��ng)ֱ��![]() ��
��![]() б�ʲ����ڕr(sh��)��
б�ʲ����ڕr(sh��)��![]() �c(di��n)����(bi��o)��
�c(di��n)����(bi��o)��![]() ��
��![]() ;
;
��(d��ng)ֱ��![]()
![]() б�ʴ��ڕr(sh��)���O(sh��)б�ʷքe��
б�ʴ��ڕr(sh��)���O(sh��)б�ʷքe��![]() , �O(sh��)
, �O(sh��)![]()
![]() ��
�� , �ã�
, �ã�
![]() , ����:
, ����:![]() ��
��![]() , �t��
, �t��
![]()
![]() . ͬ����
. ͬ����![]()
![]() , ��?y��n)?/span>
, ��?y��n)?/span>
![]() , ����
, ����![]()
![]() , ��
, ��![]() , ���}��֪
, ���}��֪![]() , ����
, ����
![]() �� �O(sh��)
�� �O(sh��)![]() ���t
���t![]() ����
����![]() ���ɮ�(d��ng)ֱ��
���ɮ�(d��ng)ֱ��![]() ��
��![]() б�ʲ����ڕr(sh��)��
б�ʲ����ڕr(sh��)��![]() �c(di��n)����(bi��o)��
�c(di��n)����(bi��o)��![]() ��
��![]() Ҳ�M��˷��̣������c(di��n)
Ҳ�M��˷��̣������c(di��n)![]() �ڙE�A
�ڙE�A![]() ��.�����c(di��n)
��.�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ����ֵ��
�鶨ֵ����ֵ��![]() .
.
���c(di��n)���A�F�����Ķ��x�����|(zh��)������.
�������c(di��n)�硿���}�nj�(du��)�A�F�����ľC�ϑ�(y��ng)���M(j��n)�п��飬��һ��ͨ�^�ɂ�(g��)����λ�ã��õ�������![]() ��
��![]() ����
����![]() ,
,![]() ,�Ķ��ÙE�A�ķ��̣��ڶ������}Ŀ���������ɶ��c(di��n)���t
,�Ķ��ÙE�A�ķ��̣��ڶ������}Ŀ���������ɶ��c(di��n)���t![]() �c(di��n)��܉�E�ǙE�A�����p���� �����}���P(gu��n)�I�Ǐ��@��(g��)�Ƕȳ��l(f��)����
�c(di��n)��܉�E�ǙE�A�����p���� �����}���P(gu��n)�I�Ǐ��@��(g��)�Ƕȳ��l(f��)����![]() ����(bi��o)�������
����(bi��o)�������![]() �c(di��n)��܉�E�����ǙE�A
�c(di��n)��܉�E�����ǙE�A![]() ���Ķ���ô��ڃɶ��c(di��n)
���Ķ���ô��ڃɶ��c(di��n)![]() ���c(di��n)
���c(di��n)![]() .
.
���}�͡�����}
���Y(ji��)����
21
���}Ŀ����֪![]() ��
��![]() ��
��![]() .
.
������![]() ����
����![]() �ĘOֵ��
�ĘOֵ��
����������(sh��)![]() �ăɂ�(g��)���c(di��n)��
�ăɂ�(g��)���c(di��n)��![]() ��ӛ
��ӛ![]() ���C����
���C����![]() ��
��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com