
【題目】設函數f(x)=x3-3ax2+3bx的圖像與直線12x+y-1=0相切于點(1,-11)。
(1)求a,b的值;
(2)討論函數f(x)的單調性.
【答案】
(1)
【解答】
解:由題意:![]() 即
即 ![]() 解得
解得![]()
(2)
【解答】
解:f'(x)=3x2-6x+9=3(x2-2x+3)=3(x-3)(x+1)
當 x<-1 或 x>3 時, f'(x)>0 , 所以f(x) 的單調遞增區間為![]() 與
與![]()
當 -1<x<3 時, f'(x)<0 , 所以f(x) 的單調遞減區間為 (-1,3)
【解析】本題主要考查了利用導數研究函數的單調性,解決問題的關鍵是根據導數的幾何意義及利用導數求函數的單調區間,屬基礎題
【考點精析】利用利用導數研究函數的單調性對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數y=x+ ![]() 有如下性質:如果常數t>0,那么該函數(0,
有如下性質:如果常數t>0,那么該函數(0, ![]() ]上是減函數,在[
]上是減函數,在[ ![]() ,+∞)上是增函數.
,+∞)上是增函數.
(1)已知f(x)= ![]() ,g(x)=﹣x﹣2a,x∈[0,1],利用上述性質,求函數f(x)的單調區間和值域.
,g(x)=﹣x﹣2a,x∈[0,1],利用上述性質,求函數f(x)的單調區間和值域.
(2)對于(1)中的函數f(x)和函數g(x),若對于任意的x1∈[0,1],總存在x2∈[0,1],使得g(x2)=f(x1)成立,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(2,8),B(x1 , y1),C(x2 , y2)在拋物線 ![]() 上,△ABC的重心與此拋物線的焦點F重合(如圖)
上,△ABC的重心與此拋物線的焦點F重合(如圖)
(1)寫出該拋物線的方程和焦點F的坐標;
(2)求線段BC中點M的坐標;
(3)求BC所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線![]() 與拋物線
與拋物線![]() 交于A、B兩點,線段AB的垂直平分線與直線y=-5交于Q點.
交于A、B兩點,線段AB的垂直平分線與直線y=-5交于Q點.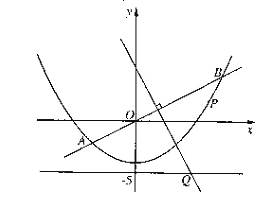
(1)求點Q的坐標;
(2)當P為拋物線上位于線段AB下方(含A、B)的動點時,求ΔOPQ面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
已知直線l:ρsin(θ+![]() )=
)=![]() m,曲線C:
m,曲線C: 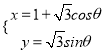
(1)當m=3時,判斷直線l與曲線C的位置關系;
(2)若曲線C上存在到直線l的距離等于![]() 的點,求實數m的范圍.
的點,求實數m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A′B′C′D′中,E是棱BC的中點,G是棱DD′的中點,則異面直線GB與B′E所成的角為( ) 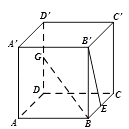
A.120°
B.90°
C.60°
D.30°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com