
【題目】如圖,四邊形ABCD為平行四邊形,四邊形ADEF是正方形,且BD⊥平面CDE,H是BE的中點,G是AE,DF的交點.

(1)求證:GH∥平面CDE;
(2)求證:面ADEF⊥面ABCD.
【答案】(1)詳見解析(2)詳見解析
【解析】
試題分析:(1)欲證GH∥平面CDE,根據(jù)直線與平面平行的判定定理可知只需證GH與平面CDE內(nèi)一直線平行,而G是AE,DF的交點,G是AE中點,又H是BE的中點,則GH∥AB,而AB∥CD,則GH∥CD,CD平面CDE,GH平面CDE,滿足定理所需條件.(2)利用線面垂直的判定定理證明ED⊥面ABCD,即可證明面AFED⊥面ABCD
試題解析:(1)∵四邊形ADEF是正方形,G是AE,DF的交點,
∴G是AE中點,
又H是BE的中點,
∴△EAB中,GH∥AB,
∵ABCD為平行四邊形
∴AB∥CD
∴GH∥CD,
又∵CD平面CDE,GH平面CDE
∴GH∥平面CDE
(2)∵BD⊥平面CDE,
∴BD⊥ED,
∵四邊形AFED為正方形,∴ED⊥AD,
∵AD∩BD=D,ED⊥面ABCD,
∵ED面AFED,
∴面AFED⊥面ABCD.


科目:高中數(shù)學 來源: 題型:
【題目】已知向量a=(x+z,3),b=(2,y-z),且a⊥b.若x,y滿足不等式|x|+|y|≤1,則z的取值范圍是__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù),且對任意的
上的偶函數(shù),且對任意的![]() ,都有
,都有![]() .當
.當![]() 時,
時,![]() .若直線
.若直線![]() 與函數(shù)
與函數(shù)![]() 的圖象有兩個不同的公共點,則實數(shù)
的圖象有兩個不同的公共點,則實數(shù)![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式.勤于思考的小紅設(shè)計了下面兩種解題思路,請你選擇其中一種并將其補充完整.
的通項公式.勤于思考的小紅設(shè)計了下面兩種解題思路,請你選擇其中一種并將其補充完整.
思路1:先設(shè)![]() 的值為1,根據(jù)已知條件,計算出
的值為1,根據(jù)已知條件,計算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用數(shù)學歸納法證明.證明過程如下:
①當![]() 時,________________,猜想成立
時,________________,猜想成立
②假設(shè)![]() (
(![]() N*)時,猜想成立,即
N*)時,猜想成立,即![]() _______.
_______.
那么,當![]() 時,由已知
時,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,兩式相減并化簡,得
,兩式相減并化簡,得![]() _____________(用含
_____________(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
所以,當![]() 時,猜想也成立.
時,猜想也成立.
根據(jù)①和②,可知猜想對任何![]() N*都成立.
N*都成立.
思路2:先設(shè)![]() 的值為1,根據(jù)已知條件,計算出
的值為1,根據(jù)已知條件,計算出![]() _____________.
_____________.
由已知![]() ,寫出
,寫出![]() 與
與![]() 的關(guān)系式:
的關(guān)系式: ![]() _____________________,
_____________________,
兩式相減,得![]() 與
與![]() 的遞推關(guān)系式:
的遞推關(guān)系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
發(fā)現(xiàn):數(shù)列![]() 是首項為________,公比為_______的等比數(shù)列.
是首項為________,公比為_______的等比數(shù)列.
得出:數(shù)列![]() 的通項公式
的通項公式![]() ____,進而得到
____,進而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知隨機變量![]() 的取值為不大于
的取值為不大于![]() 的非負整數(shù)值,它的分布列為:
的非負整數(shù)值,它的分布列為:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中![]() (
(![]() )滿足:
)滿足: ![]() ,且
,且![]() .
.
定義由![]() 生成的函數(shù)
生成的函數(shù)![]() ,令
,令![]() .
.
(I)若由![]() 生成的函數(shù)
生成的函數(shù)![]() ,求
,求![]() 的值;
的值;
(II)求證:隨機變量![]() 的數(shù)學期望
的數(shù)學期望![]() ,
, ![]() 的方差
的方差![]() ;
;
(![]() )
)
(Ⅲ)現(xiàn)投擲一枚骰子兩次,隨機變量![]() 表示兩次擲出的點數(shù)之和,此時由
表示兩次擲出的點數(shù)之和,此時由![]() 生成的函數(shù)記為
生成的函數(shù)記為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
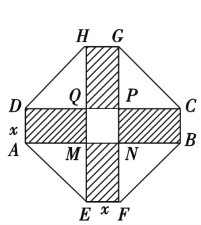
【題目】某居民小區(qū)要建造一座八邊形的休閑小區(qū),它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構(gòu)成的,是面積為200平方米的十字形地帶.計劃在正方MNPQ上建一座花壇,造價是每平方米4 200元,在四個相同的矩形(圖中陰影部分)上鋪上花崗巖地坪,造價是每平方米210元,再在四個空角上鋪上草坪,造價是每平方米80元.
(1)設(shè)總造價是S元,AD長為x米,試建立S關(guān)于x的函數(shù)關(guān)系式;
(2)當x為何值時,S最小?并求出最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com