
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍。設購進A掀電腦x臺,這100臺電腦的銷售總利潤為y元。
①求y與x的關系式;
②該商店購進A型、B型各多少臺,才能使銷售利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺。若商店保持兩種電腦的售價不變,請你以上信息及(2)中的條件,設計出使這100臺電腦銷售總利潤最大的進貨方案。
【答案】(1)每臺A型電腦的銷售利潤為100元,每臺B型電腦的銷售利潤為150元;(2)商店購進A型電腦34臺,B型電腦66臺,才能使銷售總利潤最大;(3)即商店購進70臺A型電腦和30臺B型電腦才能獲得最大利潤.
【解析】試題分析:(1)依據題設條件每臺A型電腦的銷售利潤為a元,每臺B型電腦的銷售利潤為b元建立方程組![]() 進行求解;(2)①根據題意建立目標函數y=100x+150(100-x);②根據題意建立不等式100-x≤2x進行分析求解;(3)據題意建立目標函數y=(100+m)x+150(100-x),然后運用分類整合思想對參數進行分類討論求其最大值。
進行求解;(2)①根據題意建立目標函數y=100x+150(100-x);②根據題意建立不等式100-x≤2x進行分析求解;(3)據題意建立目標函數y=(100+m)x+150(100-x),然后運用分類整合思想對參數進行分類討論求其最大值。
解:(1)設每臺A型電腦的銷售利潤為a元,每臺B型電腦的銷售利潤為b元,
則有![]() 解得
解得![]()
即每臺A型電腦的銷售利潤為100元,每臺B型電腦的銷售利潤為150元.
(2)①根據題意得y=100x+150(100-x),即y=-50x+15000
②根據題意得100-x≤2x,解得x≥33![]() ,
,
∵y=-50x+15000,-50<0,∴y隨x的增大而減小.
∵x為正整數,∴當x=34最小時,y取最大值,此時100-x=66.
即商店購進A型電腦34臺,B型電腦66臺,才能使銷售總利潤最大
(3)根據題意得y=(100+m)x+150(100-x),即y=(m-50)x+15000.
33![]() ≤x≤70.
≤x≤70.
①當0<m<50時,m-50<0,y隨x的增大而減小.
∴當x =34時,y取得最大值.
即商店購進34臺A型電腦和66臺B型電腦才能獲得最大利潤;
②當m=50時,m-50=0,y=15000.
即商店購進A型電腦數最滿足33![]() ≤x≤70的整數時,均獲得最大利潤;
≤x≤70的整數時,均獲得最大利潤;
③當50<m<100時,m-50>0,y隨x的增大而增大.
∴x=70時,y取得最大值.
即商店購進70臺A型電腦和30臺B型電腦才能獲得最大利潤.


 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】已知a是實數,函數f(x)=![]() (x-a).
(x-a).
(1)求函數f(x)的單調區間;
(2)設g(a)為f(x)在區間[0,2]上的最小值.
①寫出g(a)的表達式;
②求a的取值范圍,使得-6≤g(a)≤-2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子中裝有2個紅球,4個白球,除顏色外,它們的形狀、大小、質量等完全相同
(1)采用不放回抽樣,先后取兩次,每次隨機取一個球,求恰好取到1個紅球,七個白球的概率;
(2)采用放回抽樣,每次隨機抽取一球,連續取3次,求至少有1次取到紅球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 圖象上點
圖象上點![]() 處的切線方程與直線
處的切線方程與直線![]() 平行(其中
平行(其中![]() ),
),![]() .
.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)求函數![]() 在
在![]() (
(![]() )上的最小值;
)上的最小值;
(Ⅲ)對一切![]() ,
, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出![]() 與銷售額
與銷售額![]() (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回歸直線方程;
(2)試預測廣告費支出為![]() 萬元時,銷售額多大?
萬元時,銷售額多大?
(3)在已有的五組數據中任意抽取兩組,求至少有一組數據其預測值與實際值之差的絕對值不超過![]() 的概率.(參考數據:
的概率.(參考數據: 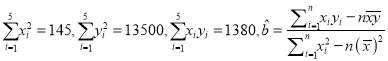 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的有( )
①函數y=![]() 的定義域為{x|x≥1};
的定義域為{x|x≥1};
②函數y=x2+x+1在(0,+∞)上是增函數;
③函數f(x)=x3+1(x∈R),若f(a)=2,則f(-a)=-2;
④已知f(x)是R上的增函數,若a+b>0,則有f(a)+f(b)>f(-a)+f(-b).
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數對![]() 一切實數
一切實數![]() 都有
都有![]() ,且當
,且當![]() 時,
時,![]() ,又
,又![]() .
.
(1)判斷該函數的奇偶性并說明理由;、
(2)試判斷該函數在![]() 上的單調性;
上的單調性;
(3)求![]() 在區間
在區間![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com