【題目】（1）橢圓C：
+
=1（a＞b＞0）與x軸交于A、B兩點，點P是橢圓C上異于A、B的任意一點，直線PA、PB分別與y軸交于點M、N，求證：
為定值b2﹣a2．
（2）由（1）類比可得如下真命題：雙曲線C：
=1（a＞0，b＞0）與x軸交于A、B兩點，點P是雙曲線C上異于A、B的任意一點，直線PA、PB分別與y軸交于點M、N，則
為定值．請寫出這個定值（不要求給出解題過程）．
【答案】（1）
；（2）
【解析】
（1）設點P（x0，y0），x0≠±a，依題意，得A（﹣a，0），B（a，0），從而得直線PA的方程，繼而求得點M，N的縱坐標，得到yMyN=
，把點P（x0，y0），代入橢圓方程可求得yMyN==b2，從而得
=b2﹣a2．
（2）類比（1）的結論，可得的值．
（1）證明：設點P（x0，y0），x0≠±a，
依題意，得A（﹣a，0），B（a，0），
∴直線PA的方程為y=
（x+a）
令x=0，得yM=
同理得yN=
∴yMyN=，
∵點P（x0，y0）是橢圓C上一點，
∴
=1，
=
（a2﹣
），
∴yMyN==b2，
=（a，yN），
=（﹣a，yM），
∴=﹣a2+yMyN=b2﹣a2
（2）﹣（a2+b2）
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如圖，橢圓 
=1（a＞b＞0）的左、右頂點分別為A，B，焦距為2 
，直線x=﹣a與y=b交于點D，且|BD|=3 ，過點B作直線l交直線x=﹣a于點M，交橢圓于另一點P．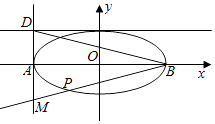 
（1）求橢圓的方程；
（2）證明： 
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lnx﹣a（x﹣1），g（x）=ex ．
（1）當a=2時，求函數f（x）的最值；
（2）當a≠0時，過原點分別作曲線y=f（x）與y=g（x）的切線l1 ， l2 ， 已知兩切線的斜率互為倒數，證明： 
＜a＜ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位為了了解用電量y度與氣溫x℃之間的關系，隨機統計了某4天的用電量與當天氣溫，并制作了對照表：
氣溫/℃ | 18 | 13 | 10 | －1 |
用電量/度 | 24 | 34 | 38 | 64 |
由表中數據得線性回歸方程
中，
≈－2，預測當氣溫為－4℃時，用電量為多少．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在人群流量較大的街道，有一中年人吆喝“送錢”，只見他手拿一黑色小布袋，袋中有3只黃色、3只白色的乒乓球（其體積、質地完成相同），旁邊立著一塊小黑板寫道：
摸球方法：從袋中隨機摸出3個球，若摸得同一顏色的3個球，攤主送給摸球者5元錢；若摸得非同一顏色的3個球，摸球者付給攤主1元錢．
（1）摸出的3個球為白球的概率是多少？
（2）摸出的3個球為2個黃球1個白球的概率是多少？
（3）假定一天中有100人次摸獎，試從概率的角度估算一下這個攤主一個月（按30天計）能賺多少錢？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sin2x+2 
sin2x+1﹣ ．
（1）求函數f（x）的最小正周期和單調遞增區間；
（2）當x∈[ 
， 
]時，若f（x）≥log2t恒成立，求t的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
