
���}Ŀ����֪��A![]() ��
��![]() ��
��![]() ��
��![]() �քe���A
�քe���A![]() �c
�c![]() �S�����ҽ��c(di��n)��ֱ��
�S�����ҽ��c(di��n)��ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() ���c
���c![]() �S��ֱ���c(di��n)
�S��ֱ���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ��v����(bi��o)��
�ϣ��v����(bi��o)��![]() �����ڰ�A
�����ڰ�A![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ʹ
ʹ![]() ���t
���t![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
���𰸡�A
��������
����(j��)�}�⣬�O(sh��)PQ�cx�S�����c(di��n)T�������ɵ���Rt��PBT�У�|BT|![]() |PB|
|PB|![]() |t|����p��x�S�Ϸ����·���x�S�����N��rӑՓ������|BT|����ֵ�����ɵ�t�ķ������C�Ͽɵô𰸣�
|t|����p��x�S�Ϸ����·���x�S�����N��rӑՓ������|BT|����ֵ�����ɵ�t�ķ������C�Ͽɵô𰸣�
����(j��)�}�⣬�O(sh��)PQ�cx�S�����c(di��n)T���t|PB|��|t|��
����BP�cx�S��ֱ���ҡ�BPQ![]() ���t��Rt��PBT�У�
���t��Rt��PBT��
|BT|![]() |PB|
|PB|![]() |t|��
|t|��
��(d��ng)P��x�S�Ϸ��r(sh��)��PT�c��A�й����c(di��n)Q��PT�c��A���Еr(sh��)��|BT|�����ֵ3���˕r(sh��)t�����ֵ![]() ��
��
��(d��ng)P��x�S�·��r(sh��)����(d��ng)Q�cA�غϕr(sh��)��|BT|�����ֵ2��|t|�����ֵ![]() ���ttȡ����Сֵ
���ttȡ����Сֵ![]() ��
��
t��0�r(sh��)��P�cB�غϣ��������}�⣬
�tt��ȡֵ������[![]() ��0��
��0��![]() ]��
]��
���x��A��



 ��(y��u)�����}��ϵ�д�
��(y��u)�����}��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����1����ֱ֪��![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() �����cֱ��
�����cֱ��![]() �ĊA�Ǟ�
�ĊA�Ǟ�![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����֪![]() ����c(di��n)
����c(di��n)![]() ��ƽ�־����̷քe��
��ƽ�־����̷քe��![]() ��
��![]() .��
.��![]() ߅���ڵ�ֱ������.
߅���ڵ�ֱ������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
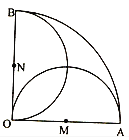
���}Ŀ����D���ڈA�ĽǞ�ֱ�ǵ�����OAB�^(q��)���У�M��N�քe��OA��OB�����c(di��n)����M��N���c(di��n)̎����һ��(g��)ͨ�Ż�վ������̖(h��o)�ĸ��w�����քe����OA��OB��ֱ���ĈA��������OAB��(n��i)�S�C(j��)ȡһ�c(di��n)���t���c(di��n)�o��̖(h��o)�ĸ�����![]() ��
��![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�p����![]() ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)��![]() ����
����![]()
��1�����p����![]() �ķ���
�ķ���
��2���O(sh��)��(j��ng)�^���c(di��n)![]() ��ֱ��
��ֱ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() ����(d��ng)ֱ��
����(d��ng)ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ�ڲ�ͬ�ă��c(di��n)
����֧�ཻ�ڲ�ͬ�ă��c(di��n)![]() �r(sh��)����(sh��)��(sh��)
�r(sh��)����(sh��)��(sh��)![]() ��ȡֵ����
��ȡֵ����
��3���O(sh��)��2����ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ��
����֧�ཻ��![]() ���c(di��n)�����Ƿ���ڌ�(sh��)��(sh��)
���c(di��n)�����Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ��
��ʹ��![]() ���J�ǣ������ڣ�Ո(q��ng)���
���J�ǣ������ڣ�Ո(q��ng)���![]() �ķ������������ڣ�Ո(q��ng)�f������
�ķ������������ڣ�Ո(q��ng)�f������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
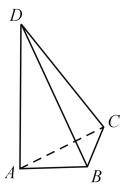
���}Ŀ����D��AD�cBC�������wABCD�л��ഹֱ���⣬BC=2. ��AD=2c����AB+BD=AC+CD=2a������a��c�鳣��(sh��)���t�����wABCD���w�e�����ֵ�� .
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() �Ķ��(xi��ng)չ�_ʽ�У������(xi��ng)�Ķ��(xi��ng)ʽϵ��(sh��)֮�͞�
�Ķ��(xi��ng)չ�_ʽ�У������(xi��ng)�Ķ��(xi��ng)ʽϵ��(sh��)֮�͞�![]() .
.
��1����չ�_ʽ�ij���(sh��)�(xi��ng)��
��2����չ�_ʽ�������攵(sh��)�(xi��ng)��ϵ��(sh��)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������f�������_�Ă�(g��)��(sh��)�ǣ� ��
�����P(gu��n)ϵ��(sh��)![]() �Á�����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����
�Á�����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����![]() Խ�ӽ���1�����P(gu��n)��Խ����
Խ�ӽ���1�����P(gu��n)��Խ����
�ڻؚwֱ��![]() �^�ӱ��c(di��n)����
�^�ӱ��c(di��n)����![]() ��
��
�����P(gu��n)ָ��(sh��)![]() �Á��̮��ؚw��Ч����
�Á��̮��ؚw��Ч����![]() ԽС���f��ģ�͵ĔM��Ч��Խ����.
ԽС���f��ģ�͵ĔM��Ч��Խ����.
A. 0B. 1C. 2D. 3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
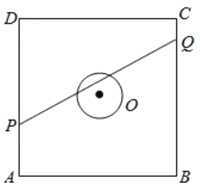
���}Ŀ����D��������![]() ��߅�L(zh��ng)��
��߅�L(zh��ng)��![]() �ף��A
�ף��A![]() �İ돽��
�İ돽��![]() �ף��A���������ε����ģ��c(di��n)
�ף��A���������ε����ģ��c(di��n)![]() ��
��![]() �քe�ھ���
�քe�ھ���![]() ��
��![]() �ϣ�������
�ϣ�������![]() �c�A
�c�A![]() ����c(di��n)���t�Q�c(di��n)
����c(di��n)���t�Q�c(di��n)![]() ���c(di��n)
���c(di��n)![]() �ġ�ä�^(q��)���У���֪�c(di��n)
�ġ�ä�^(q��)���У���֪�c(di��n)![]() ��
��![]() ��/����ٶȏ�
��/����ٶȏ�![]() ���l(f��)��
���l(f��)��![]() �Ƅ�(d��ng)��ͬ�r(sh��)���c(di��n)
�Ƅ�(d��ng)��ͬ�r(sh��)���c(di��n)![]() ��
��![]() ��/����ٶȏ�
��/����ٶȏ�![]() ���l(f��)��
���l(f��)��![]() �Ƅ�(d��ng)���t���c(di��n)
�Ƅ�(d��ng)���t���c(di��n)![]() ��
��![]() �Ƅ�(d��ng)��
�Ƅ�(d��ng)��![]() ���^���У��c(di��n)
���^�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��ä�^(q��)�еĕr(sh��)�L(zh��ng)�s________�루���_��
��ä�^(q��)�еĕr(sh��)�L(zh��ng)�s________�루���_��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
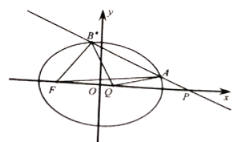
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ���x���ʞ�
���x���ʞ�![]() ���ҙE�A
���ҙE�A![]() ���S��һ��(g��)��c(di��n)��һ��(g��)���c(di��n)�ľ��x����
���S��һ��(g��)��c(di��n)��һ��(g��)���c(di��n)�ľ��x����![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)��(j��ng)�^�c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A
���E�A![]() ��
��![]() ��
��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() .
.
����(du��)����ֱ��![]() �������c(di��n)
�������c(di��n)![]() ��ʹ��
��ʹ��![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
���O(sh��)�c(di��n)![]() ��E�A
��E�A![]() �����c(di��n)�����c(di��n)
�����c(di��n)�����c(di��n)![]() ��
��![]() �����ģ���(sh��)��(sh��)
�����ģ���(sh��)��(sh��)![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com