
【題目】若正項數列![]() 滿足:
滿足:![]() ,則稱此數列為“比差等數列”.
,則稱此數列為“比差等數列”.
(1)試寫出一個“比差等數列”的前![]() 項;
項;
(2)設數列![]() 是一個“比差等數列”,問
是一個“比差等數列”,問![]() 是否存在最小值,如存在,求出最小值;如不存在,請說明理由;
是否存在最小值,如存在,求出最小值;如不存在,請說明理由;
(3)已知數列![]() 是一個“比差等數列”,
是一個“比差等數列”,![]() 為其前
為其前![]() 項的和,試證明:
項的和,試證明:![]() .
.
【答案】(1)![]() 、
、![]() 、
、![]() (答案不唯一);(2)存在,且
(答案不唯一);(2)存在,且![]() 的最小值為
的最小值為![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)根據“比差等數列”的定義得出![]() ,由
,由![]() ,可得出
,可得出![]() ,然后對
,然后對![]() 取一個大于
取一個大于![]() 的值,可得出一個符合條件的“比差等數列”
的值,可得出一個符合條件的“比差等數列”![]() 的前
的前![]() 項;
項;
(2)由題意得出![]() ,且
,且![]() ,利用基本不等式可求出
,利用基本不等式可求出![]() 的最小值;
的最小值;
(3)由![]() 可推出
可推出![]() ,利用數學歸納法證明
,利用數學歸納法證明![]() ,由此得出
,由此得出![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,然后利用同向不等式的可加性可證明出
,然后利用同向不等式的可加性可證明出![]() 成立.
成立.
(1)由于數列![]() 為“比差等數列”,則
為“比差等數列”,則![]() ,可得
,可得![]() .
.
由于數列![]() 每項都是正數,則
每項都是正數,則![]() ,可得出
,可得出![]() .
.
若![]() ,則
,則![]() ,
,![]() .
.
因此,“比差等數列”的前![]() 項可以是
項可以是![]() 、
、![]() 、
、![]() (答案不唯一);
(答案不唯一);
(2)由(1)可知,![]() ,則
,則![]() ,
,
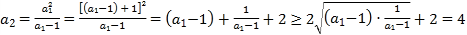 ,
,
當且僅當![]() 時,等號成立,因此,
時,等號成立,因此,![]() 有最小值
有最小值![]() ;
;
(3)由題意可得 .
.
由于雙勾函數![]() 在
在![]() 上是增函數,
上是增函數,
![]() ,
,![]() ,且
,且![]() ,則
,則![]() ,
,
同理可得![]() .
.
猜想,當![]() 時,
時,![]() .
.
假設當![]() 時,猜想成立,即
時,猜想成立,即![]() ;
;
那么當![]() 時,由于函數
時,由于函數![]() 在
在![]() 上是增函數,
上是增函數,
且![]() ,
,
所以,![]() .
.
由歸納原理可知,當![]() 時,
時,![]() .
.
于是有![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() ,
,
將上述不等式全部相加得![]() .
.
因此,![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖1,在平面四邊形![]() 中,
中,![]() ,現將
,現將![]() 沿四邊形
沿四邊形![]() 的對角線
的對角線![]() 折起,使點
折起,使點![]() 運動到點
運動到點![]() ,如圖2,這時平面
,如圖2,這時平面![]() 平面
平面![]() .
.
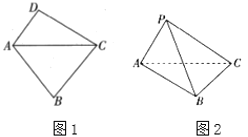
(1)求直線![]() 與平面
與平面![]() 所成角的正切值;
所成角的正切值;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了應對金融危機,決定適當進行裁員,已知這家公司現有職工![]() 人(
人(![]() ,且
,且![]() 為10的整數倍),每人每年可創利100千元,據測算,在經營條件不變的前的提下,若裁員人數不超過現有人數的30%,則每裁員1人,留崗員工每人每年就能多創利1千元(即若裁員
為10的整數倍),每人每年可創利100千元,據測算,在經營條件不變的前的提下,若裁員人數不超過現有人數的30%,則每裁員1人,留崗員工每人每年就能多創利1千元(即若裁員![]() 人,留崗員工可多創利潤
人,留崗員工可多創利潤![]() 千元);若裁員人數超過現有人數的30%,則每裁員1人,留崗員工每人每年就能多創利2千元(即若裁員
千元);若裁員人數超過現有人數的30%,則每裁員1人,留崗員工每人每年就能多創利2千元(即若裁員![]() 人,留崗員工可多創利潤
人,留崗員工可多創利潤![]() 千元),為保證公司的正常運轉,留崗的員工數不得少于現有員工人數的50%,為了保障被裁員工的生活,公司要付給被裁員工每人每年20千元的生活費.
千元),為保證公司的正常運轉,留崗的員工數不得少于現有員工人數的50%,為了保障被裁員工的生活,公司要付給被裁員工每人每年20千元的生活費.
(1)設公司裁員人數為![]() ,寫出公司獲得的經濟效益
,寫出公司獲得的經濟效益![]() (千元)關于
(千元)關于![]() 的函數(經濟效益=在職人員創利總額—被裁員工生活費);
的函數(經濟效益=在職人員創利總額—被裁員工生活費);
(2)為了獲得最大的經濟效益,該公司應裁員多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家質量監督檢驗檢疫局于2004年5月31日發布了新的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗》國家標準.新標準規定,車輛駕駛人員血液中的酒精含量大于或等于![]() 毫克/百毫升,小于
毫克/百毫升,小于![]() 毫克/百毫升為飲酒駕車,血液中的酒精含量大于或等于
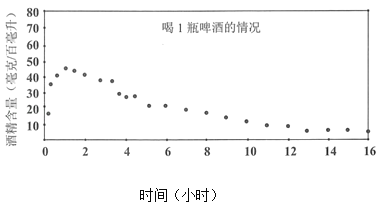
毫克/百毫升為飲酒駕車,血液中的酒精含量大于或等于![]() 毫克/百毫升為醉酒駕車.經過反復試驗,喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”如下圖,該函數近似模型如下:
毫克/百毫升為醉酒駕車.經過反復試驗,喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”如下圖,該函數近似模型如下: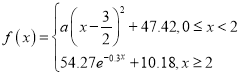 .
.
又已知剛好過1小時時測得酒精含量值為![]() 毫克/百毫升.根據上述條件,解答以下問題:
毫克/百毫升.根據上述條件,解答以下問題:
(1)試計算喝1瓶啤酒多少小時血液中的酒精含量達到最大值?最大值是多少?
(2)試計算喝1瓶啤酒后多少小時后才可以駕車?(時間以整分鐘計算)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某環線地鐵按內、外環線同時運行,內、外環線的長均為30千米(忽略內、外環線長度差異).
(1)當9列列車同時在內環線上運行時,要使內環線乘客最長候車時間為10分鐘,求內環線列車的最小平均速度;
(2)新調整的方案要求內環線列車平均速度為25千米/小時,外環線列車平均速度為30千米/小時.現內、外環線共有18列列車全部投入運行,要使內外環線乘客的最長候車時間之差不超過1分鐘,向內、外環線應各投入幾列列車運行?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() ,記該數列前
,記該數列前![]() 項
項![]() 中的最大項為
中的最大項為![]() ,即
,即![]() ,該數列后
,該數列后![]() 項
項![]() 中的最小項為
中的最小項為![]() ,記
,記![]() ,
,![]() ;
;
(1)對于數列:3,4,7,1,求出相應的![]() ,
,![]() ,
,![]() ;
;
(2)若![]() 是數列
是數列![]() 的前
的前![]() 項和,且對任意
項和,且對任意![]() ,有
,有![]() ,其中
,其中![]() 為實數,
為實數,![]() 且
且![]() ,
,![]() .
.
(ⅰ)設![]() ,證明:數列
,證明:數列![]() 是等比數列;
是等比數列;
(ⅱ)若數列![]() 對應的
對應的![]() 滿足
滿足![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 為兩非零有理數列(即對任意的
為兩非零有理數列(即對任意的![]() ,
,![]() 均為有理數),
均為有理數),![]() 為一無理數列(即對任意的
為一無理數列(即對任意的![]() ,
,![]() 為無理數).
為無理數).
(1)已知![]() ,并且
,并且![]() 對任意的
對任意的![]() 恒成立,試求
恒成立,試求![]() 的通項公式.
的通項公式.
(2)若![]() 為有理數列,試證明:對任意的
為有理數列,試證明:對任意的![]() ,
,![]() 恒成立的充要條件為
恒成立的充要條件為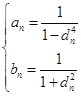 .
.
(3)已知![]() ,
,![]() ,對任意的
,對任意的![]() ,
,![]() 恒成立,試計算
恒成立,試計算![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
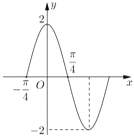
【題目】如圖是函數![]() 一個周期內的圖象,將
一個周期內的圖象,將![]() 圖象上所有點的橫坐標伸長為原來的2倍,縱坐標不變,再把所得圖象向右平移
圖象上所有點的橫坐標伸長為原來的2倍,縱坐標不變,再把所得圖象向右平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象.
的圖象.
(1)求函數![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 的所有可能的值;
的所有可能的值;
(3)求函數![]() (
(![]() 為正常數)在區間
為正常數)在區間![]() 內的所有零點之和.
內的所有零點之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com