【題目】已知函數f（x）
（k＞0）
（1）若f（x）＞m的解集為{x|x＜-3，或x＞-2}，求不等式5mx2+kx+3＞0的解集；
（2）若存在x＞3，使得f（x）＞1成立，求k的取值范圍．
【答案】（1）
（2）
【解析】試題分析：（1）根據不等式解集與對應方程根的關系：-3，-2是方程mx2-2kx+6km=0的根，即利用韋達定理得方程組，解方程組可得m,k的值，代入不等式5mx2+kx+3＞0再解一元二次不等式即可（2）不等式有解問題，一般轉化為對應函數最值問題：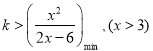 
，再根據基本不等式求最值，即得k的取值范圍．
試題解析：解：（1）不等式
，
∵不等式mx2-2kx+6km＜0的解集為{x|x＜-3，或x＞-2}，∴-3，-2是方程mx2-2kx+6km=0的根，
∴
，故有
，
∴不等式5mx2+kx+3＞0的解集為
．
（2）
．
存在x＞3，使得f（x）＞1成立，即存在x＞3，使得
成立．
令
，則k＞g（x）min．
令2x-6=t，則t∈（0，+∞），
，
當且僅當
即
時等號成立．
∴
，故k∈（6，+∞）．
優加精卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f (x)＝lg(ax2＋2x＋1) ．
(1)若函數f (x)的定義域為R，求實數a的取值范圍；
(2)若函數f (x)的值域為R，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高2010級數學培優學習小組有男生3人女生2人，這5人站成一排留影。
（1）求其中的甲乙兩人必須相鄰的站法有多少種?
（2）求其中的甲乙兩人不相鄰的站法有多少種?
（3）求甲不站最左端且乙不站最右端的站法有多少種 ?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，設傾斜角為
的直線
為參數）與曲線
為參數）相交于不同的兩點
．
（1）若
，求線段
中點
的坐標；
（2）若
，其中
，求直線
的斜率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】迭代法是用于求方程或方程組近似根的一種常用的算法設計方法．設方程為
，用某種數學方法到處等價的形式
，然后按以下步驟執行：
（1）選一個方程的近似根，賦給變量
；
（2）將
的值保存于變量
，然后計算
，并將結果存于變量
；
（3）當
與
的差的絕對值還小于指定的精度要求時，重復步驟（2）的計算．若方程有根，則按上述方法求得的
就認為是方程的根．試用迭代法求某個數的平方根，用流程圖和偽代碼表示問題的算法．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
的極坐標方程是
,以極點為平面直角坐標系的原點，極軸為
軸的正半軸, 建立平面直角坐標系，在平面直角坐標系
中, 直線
經過點
,傾斜角
．
（1）寫出曲線直角坐標方程和直線的參數方程；
（2）設與曲線相交于
兩點, 求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高一（1）班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損，可見部分如圖．
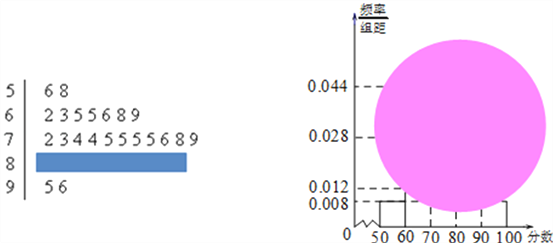
（Ⅰ）求分數在[50，60）的頻率及全班人數；
（Ⅱ）求分數在[80，90）之間的頻數，并計算頻率分布直方圖中[80，90）間矩形的高；
（Ⅲ）若要從分數在[80，100）之間的試卷中任取兩份分析學生失分情況，求在抽取的試卷中，至少有一份分數在[90，100）之間的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系中，以坐標原點為極點，
軸為正半軸建立極坐標系，圓
的極坐標方程為
，直線
的參數方程為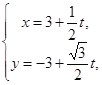
（t為參數）.
（1）求圓的直角坐標方程；
（2）求直線分圓所得的兩弧程度之比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
