若圓柱的母線與底面直徑和為3,則該圓柱的側面積的最大值為 .
【答案】
分析:由題意,可設該圓柱的底面半徑為r,母線為h依題意有2r+h=3,把側面面積用底面圓半徑r表示出來,即建立起側面面積關于底面圓半徑的函數,利用函數的相關知識求最值即可.
解答:解:設圓柱的底面半徑為r,高為h,則依題意有2r+h=3,且0<r<

.
故其側面積S=2πrh=2πr(3-2r)=4πr(

-r)≤4π×
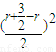
=
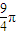
,
當且僅當r=

時,取等號.
所以圓柱的側面積的最大值等于
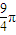
.
故答案為:
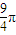
.
點評:本題考點是求旋轉體(圓柱、圓錐、圓臺)的面積、體積,考查相關的公式求表面積與體積,本題屬于中檔題.
