
【題目】設x,y,z為非零實數,滿足xy+yz+zx=1,證明:![]() .
.
【答案】不等式的證明一般可以考慮運用作差法或者是利用分析法來證明。
【解析】
試題為使所證式有意義,![]() 三數中至多有一個為0;據對稱性,不妨設
三數中至多有一個為0;據對稱性,不妨設![]() ,則
,則![]() ;
;
![]() 、當
、當![]() 時,條件式成為
時,條件式成為![]() ,
,![]() ,
,![]() ,而
,而
![]() ,
,
只要證,![]() ,即
,即![]() ,也即
,也即![]() ,此為顯然;取等號當且僅當
,此為顯然;取等號當且僅當![]() .
.
![]() 、再證,對所有滿足
、再證,對所有滿足![]() 的非負實數
的非負實數![]() ,皆有
,皆有
![]() .顯然,三數
.顯然,三數![]() 中至多有一個為0,據對稱性,
中至多有一個為0,據對稱性,
仍設![]() ,則
,則![]() ,令
,令![]() ,
,![]() 為銳角,以
為銳角,以![]() 為內角,構作
為內角,構作![]() ,則
,則![]()
![]() ,于是
,于是![]() ,且由
,且由![]() 知,
知,![]() ;于是
;于是![]() ,即
,即![]() 是一個非鈍角三角形.
是一個非鈍角三角形.
下面采用調整法,對于任一個以![]() 為最大角的非鈍角三角形
為最大角的非鈍角三角形![]() ,固定最大角
,固定最大角![]() ,將
,將![]() 調整為以
調整為以![]() 為頂角的等腰
為頂角的等腰![]() ,其中
,其中![]() ,且設
,且設![]() ,記
,記![]() ,據
,據![]() 知,
知,
![]() .今證明,
.今證明,![]() .即
.即![]()
……①.
即要證![]() ……②
……②
先證![]() ……③,即證
……③,即證![]() ,
,
即 ,此即
,此即![]() ,也即
,也即
![]() ,即
,即![]() ,此為顯然.
,此為顯然.
由于在![]() 中,
中,![]() ,則
,則![]() ;而在
;而在![]() 中,
中,
![]() ,因此②式成為
,因此②式成為
![]() ……④,
……④,
只要證,![]() ……⑤,即證
……⑤,即證![]() ,注意③式以及
,注意③式以及
![]() ,只要證
,只要證![]() ,即
,即![]() ,也即
,也即![]() …⑥
…⑥
由于最大角![]() 滿足:
滿足:![]() ,而
,而![]() ,則
,則![]() ,所以
,所以
![]() ,故⑥成立,因此⑤得證,由③及⑤得④成立,從而①成立,即
,故⑥成立,因此⑤得證,由③及⑤得④成立,從而①成立,即![]() ,因此本題得證.
,因此本題得證.


 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 相鄰兩對稱軸間的距離為
相鄰兩對稱軸間的距離為![]() ,若將
,若將![]() 的圖象先向左平移
的圖象先向左平移![]() 個單位,再向下平移1個單位,所得的函數
個單位,再向下平移1個單位,所得的函數![]() 為奇函數.
為奇函數.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的對稱中心;
的對稱中心;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不相等的實根,求實數
上有兩個不相等的實根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題16分)某鄉鎮為了進行美麗鄉村建設,規劃在長為10千米的河流OC的一側建一條觀光帶,觀光帶的前一部分為曲線段OAB,設曲線段OAB為函數![]() ,
,![]() (單位:千米)的圖象,且曲線段的頂點為
(單位:千米)的圖象,且曲線段的頂點為![]() ;觀光帶的后一部分為線段BC,如圖所示.
;觀光帶的后一部分為線段BC,如圖所示.
(1)求曲線段OABC對應的函數![]() 的解析式;
的解析式;
(2)若計劃在河流OC和觀光帶OABC之間新建一個如圖所示的矩形綠化帶MNPQ,綠化帶由線段MQ,QP, PN構成,其中點P在線段BC上.當OM長為多少時,綠化帶的總長度最長?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若二次函數f(x)=4x2-2(t-2)x-2t2-t+1在區間[-1,1]內至少存在一個值m,使得f(m)>0,則實數t的取值范圍( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了![]() 人進行分析,得到如下列聯表(單位:人).
人進行分析,得到如下列聯表(單位:人).
經常使用 | 偶爾使用或不使用 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(1)根據以上數據,能否在犯錯誤的概率不超過![]() 的前提下認為
的前提下認為![]() 市使用共享單車的情況與年齡有關;
市使用共享單車的情況與年齡有關;
(2)(i)現從所選取的![]() 歲以上的網友中,采用分層抽樣的方法選取
歲以上的網友中,采用分層抽樣的方法選取![]() 人,再從這
人,再從這![]() 人中隨機選出
人中隨機選出![]() 人贈送優惠券,求選出的
人贈送優惠券,求選出的![]() 人中至少有
人中至少有![]() 人經常使用共享單車的概率;
人經常使用共享單車的概率;
(ii)將頻率視為概率,從![]() 市所有參與調查的網友中隨機選取
市所有參與調查的網友中隨機選取![]() 人贈送禮品,記其中經常使用共享單車的人數為
人贈送禮品,記其中經常使用共享單車的人數為![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
參考公式: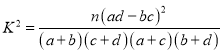 ,其中
,其中![]() .
.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,橢圓
,橢圓![]() :
:![]() 與雙曲線
與雙曲線![]() :
:![]() 的焦點相同.
的焦點相同.
(1)求橢圓![]() 與雙曲線
與雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 的右頂點作兩條斜率分別為
的右頂點作兩條斜率分別為![]() ,
,![]() 的直線
的直線![]() ,
,![]() ,分別交雙曲線
,分別交雙曲線![]() 于點
于點![]() ,
,![]() (
(![]() ,
,![]() 不同于右頂點),若
不同于右頂點),若![]() ,求證:直線
,求證:直線![]() 的傾斜角為定值,并求出此定值;
的傾斜角為定值,并求出此定值;
(3)設點![]() ,若對于直線
,若對于直線![]() ,橢圓
,橢圓![]() 上總存在不同的兩點
上總存在不同的兩點![]() 與
與![]() 關于直線
關于直線![]() 對稱,且
對稱,且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com