【題目】已知函數
，
；
(Ⅰ)若函數
在[1,2]上是減函數，求實數
的取值范圍；
(Ⅱ)令
，是否存在實數，當
(
是自然對數的底數)時，函數
的最小值是
．若存在，求出的值；若不存在，說明理由．
【答案】（Ⅰ）
；（Ⅱ）
【解析】
試題(1)
在[1,2]上恒成立
令h(x)＝2x2＋ax－1，x∈[1,2]，∴h(x)≤0在[1,2]上恒成立
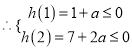得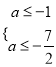
，
.
(2)假設存在實數a，使g(x)＝f(x)－x2，x∈(0，e]有最小值3
g(x)＝ax－lnx，x∈(0，e]，g′(x)＝a－
＝
①當a≤0時，g′(x)<0，g(x)在(0，e]上單調遞減
∴g(x)min＝g(e)＝ae－1＝3，∴a＝
(舍去)
②當0<
<e即a>
時，在(0，)上，g′(x)<0；在(，e]上，g′(x)>0
∴g(x)在(0，]上單調遞減，在(，e]上單調遞增
∴g(x)min＝
＝1＋lna＝3，∴a＝e2滿足條件
③當≥e即0<a≤時，g′(x)<0，g(x)在(0，e]上單調遞減
g(x)min＝g(e)＝ae－1＝3
∴a＝>(舍去)
綜上所述，存在a＝e2使得當x∈(0，e]時，g(x)有最小值3.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】《周髀算經》 是我國古代的天文學和數學著作。其中一個問題的大意為：一年有二十四個節氣（如圖），每個節氣晷長損益相同（即物體在太陽的照射下影子長度的增加量和減少量相同）．若冬至晷長一丈三尺五寸，夏至晷長一尺五寸（注：ー丈等于十尺，一尺等于十寸），則立冬節氣的晷長為（ ）
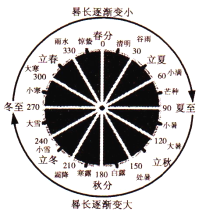
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】供電部門對某社區1000位居民2018年12月份的用電情況進行統計后，按用電量分為
，
，
，
，
五組，整理得到如下的頻率分布直方圖，則下列說法錯誤的是（ ）
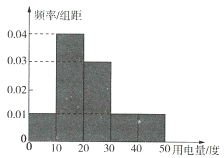
A.按用電量分組中，人數最多的一組有400人
B.12月份用電不低于20度的有500人
C.12月份人均用電量為25度
D.12月份的用電量的中位數是20度
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某中學舉行的電腦知識競賽中，將九年級兩個班參賽的學生成績（得分均為整數）進行整理后分成五組，繪制如圖所示的頻率分布直方圖.已知第二小組的頻數是40.
（1）求第二小組的頻率，并補全這個頻率分布直方圖；
（2）求這兩個班參賽的學生人數；
（3）求這兩個班參賽學生的成績的中位數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校從大二學生中隨機抽取200名學生，將其期末考試的《中西法律文化》成績（均為整數）分成六組
，
，…，
后得到如下頻率分布直方圖.
（1）求成績在
內的頻率；
（2）根據頻率分布直方圖，估計該校大二學生期末考試《中西法律文化》成績的眾數、中位數（結果保留到0.1）；
（3）用分層隨機抽樣的方法抽取一個容量為40的樣本，則各成績組應抽取的人數分別是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】太極圖是由黑白兩個魚形紋組成的圖案，俗稱陰陽魚，太極圖展現了一種相互轉化，相對統一的和諧美，定義：能夠將圓
的周長和面積同時等分成兩個部分的函數稱為圓
的一個“太極函數”，則下列有關說法中：
①對于圓
的所有非常數函數的太極函數中，一定不能為偶函數；
②函數
是圓
的一個太極函數；
③存在圓
，使得
是圓
的一個太極函數；
④直線
所對應的函數一定是圓
的太極函數；
⑤若函數
是圓
的太極函數，則
所有正確的是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校開設了射擊選修課，規定向
、
兩個靶進行射擊：先向靶射擊一次，命中得1分，沒有命中得0分，向靶連續射擊兩次，每命中一次得2分，沒命中得0分；小明同學經訓練可知：向靶射擊，命中的概率為
，向靶射擊，命中的概率為
，假設小明同學每次射擊的結果相互獨立.現對小明同學進行以上三次射擊的考核.
（1）求小明同學恰好命中一次的概率；
（2）求小明同學獲得總分
的分布列及數學期望
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
