
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為 ![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為
為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為 ![]() .
.
(1)求曲線C1 , C2的直角坐標方程;
(2)已知點P,Q分別是線C1 , C2的動點,求|PQ|的最小值.
 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】下列說法正確的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
B. “![]() 且
且![]() 為真命題”是“
為真命題”是“![]() 或
或![]() 為真命題” 的必要不充分條件
為真命題” 的必要不充分條件
C. 命題“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命題![]() :“
:“![]() ”,則
”,則![]() 是真命題
是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的各項均為正數,a1=3,前n項和為Sn,{bn}為等比數列,b1=1,且b2S2=64,b3S3=960.
(1)求an與bn;
(2)求![]()
【答案】(1)an=2n+1,bn=8n-1.(2)![]()
【解析】
(1)設{an}的公差為d,{bn}的公比為q,由題設條件建立方程組,解方程組得到d和q的值,從而求出an與bn;(2)由Sn=n(n+2),知![]() ,由此可求出
,由此可求出![]() 的值.
的值.
(1)設{an}的公差為d,{bn}的公比為q,則d為正數,
an=3+(n-1)d,bn=qn-1,
依題意有![]() ,
,
解得![]() 或
或 (舍去).
(舍去).
故an=3+2(n-1)=2n+1,bn=8n-1.
(2)Sn=3+5+…+(2n+1)=n(n+2).
所以![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (1-
(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() )
)
=![]() (1+
(1+![]() -
-![]() -
-![]() )
)
=![]() -
-![]() .
.
【點睛】
這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
【題型】解答題
【結束】
21
【題目】已知函數f(x)滿足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)當n∈N+,求f(n)的表達式;
(2)設an=nf(n),n∈N+,求證:a1+a2+…+an<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知有限集![]() ,如果A中元素
,如果A中元素![]() ,滿足
,滿足![]() ,就稱A為
,就稱A為![]() 元“創新集”;
元“創新集”;
(1)若![]() ,試寫出一個二元“創新集”A;
,試寫出一個二元“創新集”A;
(2)若![]() ,且
,且![]() 是二元“創新集”,求
是二元“創新集”,求![]() 的取值范圍;
的取值范圍;
(3)若![]() 是正整數,求出所有的“創新集”
是正整數,求出所有的“創新集”![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x),滿足  ,且f(3)=f(1)﹣1.
,且f(3)=f(1)﹣1.
(1)求實數k的值;
(2)若函數g(x)=f(x)+f(﹣x)(﹣2≤x≤2),求g(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos(ωx﹣φ)(ω>0,φ∈[0,π])的部分圖象如圖所示,若A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ).則下列說法錯誤的是( )
).則下列說法錯誤的是( ) 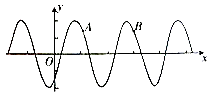
A.φ= ![]()
B.函數f(x)的一條對稱軸為x= ![]()
C.為了得到函數y=f(x)的圖象,只需將函數y=2sin2x的圖象向右平移 ![]() 個單位
個單位
D.函數f(x)的一個單調減區間為[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)(x∈R)d的導函數為f′(x),若f(x)﹣f(﹣x)=2x3 , 且當x≥0時,f′(x)>3x2 , 則不等式f(x)﹣f(x﹣1)>3x2﹣3x+1的解集是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com