
【題目】已知函數 ![]() (a<0). (Ⅰ)當a=﹣3時,求f(x)的單調遞減區間;
(a<0). (Ⅰ)當a=﹣3時,求f(x)的單調遞減區間;
(Ⅱ)若函數f(x)有且僅有一個零點,求實數a的取值范圍.
【答案】解:(Ⅰ)∵a=﹣3,∴ ![]() ,
,
故 ![]() ,
,
令f′(x)<0,解得﹣3<x<﹣2或x>0,
即所求的單調遞減區間為(﹣3,﹣2)和(0,+∞);
(Ⅱ)∵ ![]() (x>a),
(x>a),
令f′(x)=0,得x=0或x=a+1,
當a+1>0,即﹣1<a<0時,
f(x)在(a,0)和(a+1,+∞)上為減函數,在(0,a+1)上為增函數,
由于f(0)=aln(﹣a)>0,當x→a時,f(x)→+∞,
當x→+∞時,f(x)→﹣∞,于是可得函數f(x)圖象的草圖如圖:
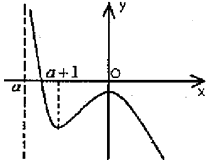
此時函數f(x)有且僅有一個零點.
即當﹣1<a<0對,f(x)有且僅有一個零點;
當a=﹣1時, ![]() ,
,
∵ ![]() ,∴f(x)在(a,+∞)單調遞減,
,∴f(x)在(a,+∞)單調遞減,
又當x→﹣1時,f(x)→+∞.當x→+∞時,f(x)→﹣∞,
故函數f(x)有且僅有一個零點;
當a+1<0即a<﹣1時,
f(x)在(a,a+1)和(0,+∞)上為減函數,在(a+1,0)上為增函數,
又f(0)=aln(﹣a)<0,當x→a時,f(x)→+∞,當x→+∞時,f(x)→﹣∞,
于是可得函數f(x)圖象的草圖如圖:
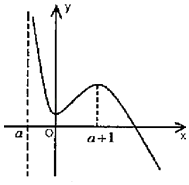
此時函數f(x)有且僅有一個零點;
綜上所述,所求的范圍是a<0.
【解析】(Ⅰ)求出函數的導數,解關于導函數的不等式,求出函數的遞減區間即可;(Ⅱ)求出函數的導數,通過討論a的范圍,求出函數的單調區間,結合函數的圖象求出a的具體范圍即可.
【考點精析】利用利用導數研究函數的單調性和函數的極值與導數對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


科目:高中數學 來源: 題型:
【題目】如圖,在底面為平行四邊形的四棱錐P﹣ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,點E是PD的中點. 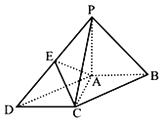
(1)求證:AC⊥PB;
(2)當二面角E﹣AC﹣D的大小為45°時,求AP的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下圖所示,圓柱的高為2,底面半徑為![]() ,AE、DF是圓柱的兩條母線,過
,AE、DF是圓柱的兩條母線,過![]() 作圓柱的截面交下底面于
作圓柱的截面交下底面于![]() ,四邊形ABCD是正方形.
,四邊形ABCD是正方形.
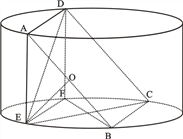
(1)求證![]() ;
;
(2)求四棱錐E-ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D為線段AC的中點.

(1)求證:PA⊥BD.
(2)求證:BD⊥平面PAC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三人獨立破譯同一份密碼.已知三人各自破譯出密碼的概率分別為 ![]() ,且他們是否破譯出密碼互不影響. (Ⅰ)求恰有二人破譯出密碼的概率;
,且他們是否破譯出密碼互不影響. (Ⅰ)求恰有二人破譯出密碼的概率;
(Ⅱ)“密碼被破譯”與“密碼未被破譯”的概率哪個大?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人口問題是當今世界各國普遍關注的問題.認識人口數量的變化規律,可以為有效控制人口增長提供依據.早在1798年,英國經濟學家馬爾薩斯(T.R.Malthus,1766—1834)就提出了自然狀態下的人口增長模型: ![]() ,其中x表示經過的時間,
,其中x表示經過的時間, ![]() 表示x=0時的人口,r表示人口的平均增長率.
表示x=0時的人口,r表示人口的平均增長率.
下表是1950―1959年我國人口數據資料:

如果以各年人口增長率的平均值作為我國這一時期的人口增長率,用馬爾薩斯人口增長模型建立我國這一時期的具體人口增長模型,某同學利用圖形計算器進行了如下探究:
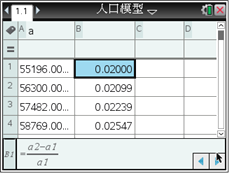
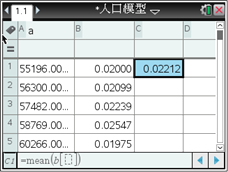
由此可得到我國1950―1959年我國這一時期的具體人口增長模型為____________. (精確到0.001)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 f(x)=x﹣ln x﹣2.
(Ⅰ)求函數 f ( x)的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在區間(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com