
【題目】已知圓![]() 與
與![]() 軸相切于點
軸相切于點![]() ,且被
,且被![]() 軸所截得的弦長為
軸所截得的弦長為![]() ,圓心
,圓心![]() 在第一象限.
在第一象限.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)若點![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作圓
作圓![]() 的切線,切點為
的切線,切點為![]() ,當(dāng)△
,當(dāng)△![]() 的面積最小時,求切線
的面積最小時,求切線![]() 的方程.
的方程.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】
(Ⅰ)由題意設(shè)圓心坐標(biāo)為(a,1),則半徑為r=a(a>0),再由圓被x軸所截得的弦長為2![]() ,利用垂徑定理求得a=2,則圓C的方程可求;
,利用垂徑定理求得a=2,則圓C的方程可求;
(Ⅱ)P為直線l:2x+y+5=0上的動點,過P作圓C的切線,切點為B,可知,要使△PBC的面積最小,則|PB|最小,也就是|PC|最小,此時CP⊥l,求出CP所在直線方程,與直線l聯(lián)立解得P(﹣2,﹣1),設(shè)切線方程為y+1=k(x+2),即kx﹣y+2k﹣1=0,再由圓心到切線的距離等于半徑求得k,則切線PB的方程可求.
解:(Ⅰ)依題意,可設(shè)圓心![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,其中
,其中![]() ,圓
,圓![]() 的半徑為
的半徑為![]() ,
,
因為圓![]() 被
被![]() 軸所截得的弦長為
軸所截得的弦長為![]() ,
,
又點![]() 到
到![]() 軸的距離為
軸的距離為![]() ,
,
則![]() ,
,
解得![]() .
.
所以圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)因為△![]() 的面積
的面積![]()
![]() .
.
故當(dāng)![]() 最小時,△
最小時,△![]() 的面積最小.
的面積最小.
由于點![]() 是直線
是直線![]() 上的動點,
上的動點,
則當(dāng)![]() 時,
時,![]() 最小.
最小.
由于直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的斜率為
的斜率為![]() .
.
直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
由![]() 解得
解得![]()
所以點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
由于直線![]() 是圓
是圓![]() 的切線,
的切線,
則點![]() 到直線
到直線![]() 的距離等于圓
的距離等于圓![]() 的半徑,即
的半徑,即![]() .
.
解得![]() 或
或![]() .
.
所以切線![]() 的方程為
的方程為![]() 或
或![]() .
.
另法:(Ⅰ)依題意,可設(shè)圓心![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,其中
,其中![]() ,圓
,圓![]() 的半徑為
的半徑為![]() ,
,
則圓![]() 的方程為
的方程為![]() .
.
令![]() ,得
,得![]()
因為圓![]() 被
被![]() 軸所截得的弦長為
軸所截得的弦長為![]() ,
,
則![]() ,
,
解得![]() .所以圓
.所以圓![]() 的方程為
的方程為![]()
(Ⅱ)因為△![]() 的面積
的面積![]()
![]() .
.
故當(dāng)![]() 最小時,△
最小時,△![]() 的面積最小.
的面積最小.
由于點![]() 是直線
是直線![]() 上的動點,設(shè)點
上的動點,設(shè)點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
則![]()
![]() .
.
當(dāng)![]() 時,
時,![]() 取得最小值,此時點
取得最小值,此時點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
由于直線![]() 是圓
是圓![]() 的切線,
的切線,
則點![]() 到直線
到直線![]() 的距離等于圓
的距離等于圓![]() 的半徑,即
的半徑,即![]() .
.
解得![]() 或
或![]() .
.
所以切線![]() 的方程為
的方程為![]() 或
或![]() .
.


 輕松暑假總復(fù)習(xí)系列答案
輕松暑假總復(fù)習(xí)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 在拋物線
在拋物線![]() 上,則當(dāng)點
上,則當(dāng)點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到拋物線焦點距離之和取得最小值時,點
到拋物線焦點距離之和取得最小值時,點![]() 的坐標(biāo)為( )
的坐標(biāo)為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】求滿足下列條件的橢圓或雙曲線的標(biāo)準(zhǔn)方程:
(1)橢圓的焦點在![]() 軸上,焦距為4,且經(jīng)過點
軸上,焦距為4,且經(jīng)過點![]() ;
;
(2)雙曲線的焦點在![]() 軸上,右焦點為
軸上,右焦點為![]() ,過
,過![]() 作重直于
作重直于![]() 軸的直線交雙曲線于
軸的直線交雙曲線于![]() ,
,![]() 兩點,且
兩點,且![]() ,離心率為
,離心率為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E:![]() 的焦距為2
的焦距為2![]() ,一條準(zhǔn)線方程為x=
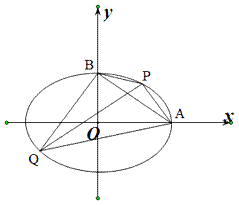
,一條準(zhǔn)線方程為x=![]() ,A,B分別為橢圓的右頂點和上頂點,點P,Q在的橢圓上,且點P在第一象限.
,A,B分別為橢圓的右頂點和上頂點,點P,Q在的橢圓上,且點P在第一象限.
(1)求橢圓E的標(biāo)準(zhǔn)方程;
(2)若點P,Q關(guān)于坐標(biāo)原點對稱,且PQ⊥AB,求四邊形ABCD的面積;
(3)若AP,BQ的斜率互為相反數(shù),求證:PQ斜率為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》是我國古代一部重要的數(shù)學(xué)著作,書中有如下問題:“今有良馬與駑馬發(fā)長安,至齊.齊去長安三千里,良馬初日行一百九十三里,日增一十三里,駑馬初日行九十七里,日減半里.良馬先至齊,復(fù)還迎駑馬,問幾何日相逢.”其大意為:“現(xiàn)在有良馬和駑馬同時從長安出發(fā)到齊去,已知長安和齊的距離是3000里,良馬第一天行193里,之后每天比前一天多行13里,駑馬第一天行97里,之后每天比前一天少行0.5里.良馬到齊后,立刻返回去迎駑馬,多少天后兩馬相遇.”試確定離開長安后的第天,兩馬相逢.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線 ![]() ,若圓上恰好存在兩個點
,若圓上恰好存在兩個點 ![]() ,
,![]() ,他們到直線
,他們到直線 ![]() 的距離為
的距離為 ![]() ,則稱該圓為“完美型”圓.則下列圓中是“完美型”圓的是
,則稱該圓為“完美型”圓.則下列圓中是“完美型”圓的是 ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com