
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)的離心率為
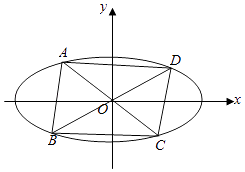
=1(a>b>0)的離心率為 ![]() ,四邊形ABCD的各頂點均在橢圓E上,且對角線AC,BD均過坐標原點O,點D(2,1),AC,BD的斜率之積為
,四邊形ABCD的各頂點均在橢圓E上,且對角線AC,BD均過坐標原點O,點D(2,1),AC,BD的斜率之積為 ![]() .
.
(Ⅰ)求橢圓E的方程;
(Ⅱ)過D作直線l平行于AC.若直線l′平行于BD,且與橢圓E交于不同的兩點M.N,與直線l交于點P.
⑴證明:直線l與橢圓E有且只有一個公共點;
⑵證明:存在常數λ,使得|PD|2=λ|PM||PN|,并求出λ的值.
【答案】解:(Ⅰ)由題意 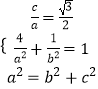 ,解得
,解得 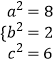 .
.
故橢圓E的方程為 ![]() ;
;
證明:(Ⅱ)(1)由題意 ![]() ,
,
∵ ![]() ,得
,得 ![]() ,則直線l的方程為
,則直線l的方程為 ![]() ,
,
聯立 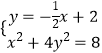 ,化簡得x2﹣4x+4=0.
,化簡得x2﹣4x+4=0.
∵判別式△=0,∴直線l與橢圓E有且只有一個公共點;
⑵設直線l′的方程為y= ![]() (m≠0).
(m≠0).
聯立方程組 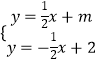 ,解得
,解得 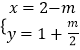 .故點P坐標為(2﹣m,
.故點P坐標為(2﹣m, ![]() ),
), ![]() .
.
聯立方程組 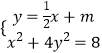 ,化簡得x2+2mx+2m2﹣4=0.
,化簡得x2+2mx+2m2﹣4=0.
設點M(x1,y1),N(x2,y2).
判別式△=4(﹣m2+4)>0,得﹣2<m<2.
又 ![]() .
.
∴|PM|= ![]() .
.
同理, ![]() .
.
故|PM||PN|= ![]() =
= ![]() =
= ![]() .
.
∵|PD|2=λ|PM||PN|,解得λ=1.
故存在常數λ為1,使得|PD|2=λ|PM||PN|.
【解析】1、(Ⅰ)本題考查的是用待定系數法求橢圓的方程。
(Ⅱ) 由題意 k A C k B D = 1 4 ,∵ ![]() ,得
,得 ![]() ,則直線l的方程為
,則直線l的方程為 ![]() ,
,
聯立 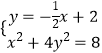 ,化簡得x2﹣4x+4=0.∵判別式△=0,∴直線l與橢圓E有且只有一個公共點;
,化簡得x2﹣4x+4=0.∵判別式△=0,∴直線l與橢圓E有且只有一個公共點;
2、聯立兩直線的方程可得故點P坐標為(2﹣m, 1 + ![]() ),
),![]() .再聯立直線和橢圓的方程化簡得x2+2mx+2m2﹣4=0.
.再聯立直線和橢圓的方程化簡得x2+2mx+2m2﹣4=0.
設點M(x1,y1),N(x2,y2).判別式△=4(﹣m2+4)>0,得﹣2<m<2.又 ![]() .
.
∴|PM|= ( 2 m x 1) 2 + ( 1 + m 2 y 1) 2 = ![]() | 2 m x 1 |即
| 2 m x 1 |即![]() .故|PM||PN|=
.故|PM||PN|= ![]() .
.
∵|PD|2=λ|PM||PN|,解得λ=1.故存在常數λ為1,使得|PD|2=λ|PM||PN|.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣2)ex﹣ ![]() x2 , 其中a∈R,e為自然對數的底數
x2 , 其中a∈R,e為自然對數的底數
(Ⅰ)函數f(x)的圖象能否與x軸相切?若能與x軸相切,求實數a的值;否則,請說明理由;
(Ⅱ)若函數y=f(x)+2x在R上單調遞增,求實數a能取到的最大整數值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)= ![]() . (a>0且a≠1),函數g(x)=f(x)﹣k.
. (a>0且a≠1),函數g(x)=f(x)﹣k.
①若a= ![]() ,函數g(x)無零點,則實數k的取值范圍為;
,函數g(x)無零點,則實數k的取值范圍為;
②若f(x)有最小值,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn , 數列{bn}是等比數列,滿足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求數列{an}和{bn}的通項公式;
(2)令cn=anbn , 設數列{cn}的前n項和為Tn , 求Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線y=x+a與拋物線y2=5ax(a>0)相交于A,B兩點,C(0,2a),給出下列4個命題:
p1:△ABC的重心在定直線7x﹣3y=0上,p2:|AB| ![]() 的最大值為2
的最大值為2 ![]() ;
;
p3:△ABC的重心在定直線 3x﹣7y=0上;p4:|AB| ![]() 的最大值為2
的最大值為2 ![]() .
.
其中的真命題為( )
A.p1 , p2
B.p1 , p4
C.p2 , p3
D.p3 , p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直角坐標平面內的兩個不同點 ![]() 、
、 ![]() 滿足條件:①
滿足條件:① ![]() 、
、 ![]() 都在函數
都在函數 ![]() 的圖像上;②
的圖像上;② ![]() 、
、 ![]() 關于原點對稱,則稱點對
關于原點對稱,則稱點對 ![]() 是函數
是函數 ![]() 的一對“友好點對”(注:點對
的一對“友好點對”(注:點對 ![]() 與
與 ![]() 看作同一對“友好點對”).已知函數
看作同一對“友好點對”).已知函數 ![]()
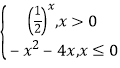 ,則此函數的“友好點對”有( )對.
,則此函數的“友好點對”有( )對.
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com