
【題目】已知橢圓 ![]() 的離心率
的離心率 ![]() ,連接橢圓的四個頂點得到的菱形的面積為4.
,連接橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程;
(2)設直線l與橢圓相交于不同的兩點A,B,已知點A的坐標為(﹣a,0),點Q(0,y0)在線段AB的垂直平分線上,且 ![]() ,求y0的值.
,求y0的值.
【答案】
(1)解:由e= ![]() ,得3a2=4c2.
,得3a2=4c2.
再由c2=a2﹣b2,解得a=2b.
由題意可知 ![]() ,即ab=2.
,即ab=2.
解方程組 ![]() 得a=2,b=1.
得a=2,b=1.
所以橢圓的方程為 ![]()
(2)解:由(Ⅰ)可知點A的坐標是(﹣2,0).
設點B的坐標為(x1,y1),直線l的斜率為k.
則直線l的方程為y=k(x+2).
于是A、B兩點的坐標滿足方程組 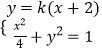
消去y并整理,得(1+4k2)x2+16k2x+(16k2﹣4)=0.
由 ![]() ,得
,得 ![]() .從而
.從而 ![]() .
.
所以 ![]() .
.
設線段AB的中點為M,
則M的坐標為 ![]() .
.
以下分兩種情況:
①當k=0時,點B的坐標是(2,0),
線段AB的垂直平分線為y軸,
于是 ![]() .
.
由 ![]() ,得
,得 ![]() .
.
②當k≠0時,線段AB的垂直平分線方程為
![]() .
.
令x=0,解得 ![]() .
.
由 ![]() ,
, ![]() ,
,
![]()
= ![]()
= ![]() ,
,
整理得7k2=2.故 ![]() .
.
所以 ![]() .
.
綜上, ![]() 或
或 ![]()
【解析】(1)由離心率求得a和c的關系,進而根據(jù)c2=a2﹣b2求得a和b的關系,進而根據(jù) ![]() 求得a和b,則橢圓的方程可得.(2)由(1)可求得A點的坐標,設出點B的坐標和直線l的斜率,表示出直線l的方程與橢圓方程聯(lián)立,消去y,由韋達定理求得點B的橫坐標的表達式,進而利用直線方程求得其縱坐標表達式,表示出|AB|進而求得k,則直線的斜率可得.設線段AB的中點為M,當k=0時點B的坐標是(2,0),線段AB的垂直平分線為y軸,進而根據(jù)
求得a和b,則橢圓的方程可得.(2)由(1)可求得A點的坐標,設出點B的坐標和直線l的斜率,表示出直線l的方程與橢圓方程聯(lián)立,消去y,由韋達定理求得點B的橫坐標的表達式,進而利用直線方程求得其縱坐標表達式,表示出|AB|進而求得k,則直線的斜率可得.設線段AB的中點為M,當k=0時點B的坐標是(2,0),線段AB的垂直平分線為y軸,進而根據(jù) ![]() 求得y0;當k≠0時,可表示出線段AB的垂直平分線方程,令x=0得到y(tǒng)0的表達式根據(jù)
求得y0;當k≠0時,可表示出線段AB的垂直平分線方程,令x=0得到y(tǒng)0的表達式根據(jù) ![]() 求得y0;綜合答案可得.
求得y0;綜合答案可得.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}中,a1=1,a1+2a2+3a3+…+nan= ![]() (n≥1,n∈Z)
(n≥1,n∈Z)
(1)求數(shù)列{an}的通項公式an;
(2)求數(shù)列{n2an}的前n項和Tn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題正確的是( )
A.一條直線與一個平面平行,它就和這個平面內的任意一條直線平行
B.平行于同一個平面的兩條直線平行
C.與兩個相交平面的交線平行的直線,必平行于這兩個平面
D.平面外兩條平行直線中的一條與這個平面平行,則另一條也與這個平面平行
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小五、小一、小節(jié)、小快、小樂五位同學站成一排,若小一不出現(xiàn)在首位和末位,小五、小節(jié)、小樂中有且僅有兩人相鄰,求能滿足條件的不同排法共有多少種?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列關于棱錐、棱臺的說法,其中不正確的是( )
A.棱臺的側面一定不會是平行四邊形
B.棱錐的側面只能是三角形
C.由四個面圍成的封閉圖形只能是三棱錐
D.棱錐被平面截成的兩部分不可能都是棱錐
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,一個樹形圖依據(jù)下列規(guī)律不斷生長:1個空心圓點到下一行僅生長出1個實心圓點,1個實心圓點到下一行生長出1個實心圓點和1個空心圓點.則第11行的實心圓點的個數(shù)是 . 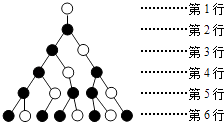
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校調查了200名學生每周的自習時間(單位:小時),制成了如圖所示的頻率分布直方圖,其中自習時間的范圍是[17.5,30],樣本數(shù)據(jù)分組為[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根據(jù)直方圖,這200名學生中每周的自習時間不少于22.5小時的人數(shù)是( )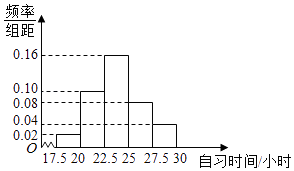
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】要得到函數(shù)y=3cosx的圖象,只需將函數(shù)y=3sin(2x﹣ ![]() )的圖象上所有點的( )
)的圖象上所有點的( )
A.橫坐標縮短到原來的 ![]() (縱坐標不變),所得圖象再向左平移
(縱坐標不變),所得圖象再向左平移 ![]() 個單位長度
個單位長度
B.橫坐標縮短到原來的 ![]() (縱坐標不變),所得圖象再向右平移
(縱坐標不變),所得圖象再向右平移 ![]() 個單位長度
個單位長度
C.橫坐標伸長到原來的2倍(縱坐標不變),所得圖象再向左平移 ![]() 個單位長度
個單位長度
D.橫坐標伸長到原來的2倍(縱坐標不變),所得圖象再向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某單位為了了解辦公樓用電量y(度)與氣溫x(℃)之間的關系,隨機統(tǒng)計了四個工作日的用電量與當天平均氣溫,并制作了對照表:
氣溫(℃) | 17 | 14 | 11 | ﹣2 |
用電量(度) | 23 | 35 | 39 | 63 |
由表中數(shù)據(jù)得到線性回歸方程 ![]() =﹣2x+a,當氣溫為﹣5℃時,預測用電量約為 ( )
=﹣2x+a,當氣溫為﹣5℃時,預測用電量約為 ( )
A.38度
B.50度
C.70度
D.30度
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com