
【題目】在等比數列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3與a5的等比中項為2.
(1)求數列{an}的通項公式;
(2)設bn=log2an , 數列{bn}的前n項和為Sn , 當 ![]() 最大時,求n的值.
最大時,求n的值.
【答案】
(1)解:因為a1a5+2a3a5+a2a8=25,所以,a32+2a3a5+a52=25
又an>o,a3+a5=5,
又a3與a5的等比中項為2,所以,a3a5=4
而q∈(0,1),所以,a3>a5,所以,a3=4,a5=1,q= ![]() ,a1=16,
,a1=16,
所以,an=16× ![]() =25﹣n
=25﹣n
(2)解:bn=log2an=5﹣n,所以,bn+1﹣bn=﹣1,
所以,{bn}是以4為首項,﹣1為公差的等差數列
所以sn= ![]()
![]() =
= ![]()
所以,當n≤8時, ![]() >0,
>0,
當n=9時, ![]() =0,
=0,
n>9時, ![]() <0,
<0,
當n=8或9時, ![]() 最大
最大
【解析】(1)利用等比數列的性質把a1a5+2a3a5+a2a8=25轉化為a32+2a3a5+a52=25,求出a3+a5=5,再利用a3與a5的等比中項為2即可首項和公比,進而求出數列{an}的通項公式;(2)先利用(1)求出數列{bn}的通項公式以及前n項和為Sn , ,進而得到 ![]() 的通項,即可求出當
的通項,即可求出當 ![]() 最大時,對應n的值.
最大時,對應n的值.
【考點精析】利用等差數列的性質對題目進行判斷即可得到答案,需要熟知在等差數列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數列是等差數列.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+21nx.
(1)求f(x)的單調區間.
(2)若f(x)在(0,1]上的最大值是﹣2,求a的值.
(3)記g(x)=f(x)+(a﹣1)lnx+1,當a≤﹣2時,若對任意x1 , x2∈(0,+∞),總有|g(x1)﹣g(x2)|≥k|x1﹣x2|成立,試求k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一(1)班全體男生的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如圖所示,據此解答如下問題:

(1)求該班全體男生的人數;
(2)求分數在![]() 之間的男生人數,并計算頻率分布直方圖中
之間的男生人數,并計算頻率分布直方圖中![]() 之間的矩形的高.
之間的矩形的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,﹣1),B(4,0),C(2,2),平面區域D是所有滿足 ![]() =
= ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的點P(x,y)組成的區域.若區域D的面積為8,則4a+b的最小值為 ( )
(1<λ≤a,1<μ≤b)的點P(x,y)組成的區域.若區域D的面積為8,則4a+b的最小值為 ( )
A.5
B.4 ![]()
C.9
D.5+4 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校有線網絡同時提供A、B兩套校本選修課程。A套選修課播40分鐘,課后研討20分鐘,可獲得學分5分B套選修課播32分鐘,課后研討40分鐘,可獲學分4分。全學期20周,網絡每周開播兩次,每次均為獨立內容。學校規定學生每學期收看選修課不超過1400分鐘,研討時間不得少于1000分鐘。兩套選修課怎樣合理選擇,才能獲得最好學分成績?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}中,已知a1=2,a4=16.
(1)求數列{an}的通項公式an;
(2)若a3 , a5分別是等差數列{bn}的第4項和第16項,求數列{bn}的通項公式及前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}為等差數列,且a5=14,a7=20,數列{bn}的前n項和為Sn , b1= ![]() 且3Sn=Sn﹣1+2(n≥2,n∈N).
且3Sn=Sn﹣1+2(n≥2,n∈N).
(Ⅰ)求數列{an},{bn}的通項公式;
(Ⅱ)若cn=anbn , n=1,2,3,…,Tn為數列{cn}的前n項和,Tn<m對n∈N*恒成立,求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
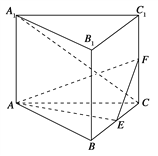
【題目】(2015·湖南)如下圖,直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,E、F分別是BC、CC1的中點.
(1)證明:平面AEF⊥平面B1BCC1;
(2)若直線A1C與平面A1ABB1所成的角為45°,求三棱錐F-AEC的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com