
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,
,![]() 是
是![]() 上一點,直線
上一點,直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,若
兩點,若![]() ,則
,則![]() =
=
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
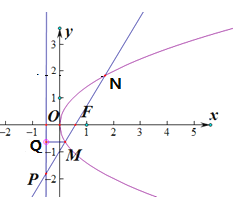
先根據題意寫出直線的方程,再將直線的方程與拋物線y2=2x的方程組成方程組,消去y得到關于x的二次方程,最后利用根與系數的關系結合拋物線的定義即可求線段AB的長.
解:拋物線C:y2=2x的焦點為F(![]() ,0),準線為l:x=﹣
,0),準線為l:x=﹣![]() ,設M(x1,y1),N(x2,y2),M,N到準線的距離分別為dM,dN,
,設M(x1,y1),N(x2,y2),M,N到準線的距離分別為dM,dN,
由拋物線的定義可知|MF|=dM=x1+![]() ,|NF|=dN=x2+
,|NF|=dN=x2+![]() ,于是|MN|=|MF|+|NF|=x1+x2+1.
,于是|MN|=|MF|+|NF|=x1+x2+1.
∵![]() ,則
,則![]() ,易知:直線MN的斜率為±
,易知:直線MN的斜率為±![]() ,
,
∵F(![]() ,0),
,0),
∴直線PF的方程為y=±![]() (x﹣
(x﹣![]() ),
),
將y=±![]() (x﹣
(x﹣![]() ),代入方程y2=2x,得3(x﹣
),代入方程y2=2x,得3(x﹣![]() )2=2x,化簡得12x2﹣20x+3=0,
)2=2x,化簡得12x2﹣20x+3=0,
∴x1+x2![]() ,于是|MN|=x1+x2+1
,于是|MN|=x1+x2+1![]() 1
1![]()
故選:B.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元,未售出的產品,每盒虧損
元,未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示.該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒,![]() )表示這個開學季內的市場需求量,
)表示這個開學季內的市場需求量,![]() (單位:元)表示這個開學季內經銷該產品的利潤.
(單位:元)表示這個開學季內經銷該產品的利潤.

(1)根據直方圖估計這個開學季內市場需求量![]() 的眾數和平均數;
的眾數和平均數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市創衛辦為了了解該市開展創衛活動的成效,對市民進行了一次創衛滿意程度測試,根據測試成績評定“合格”、“不合格”兩個等級,同時對相應等級進行量化:“合格”計5分,“不合格”計0分,現隨機抽取部分市民的回答問卷,統計結果及對應的頻率分布直方圖如圖所示:
等級 | 不合格 | 合格 | ||
得分 |
|
|
|
|
頻數 | 6 |
| 24 |
|

(1)求![]() 的值;
的值;
(2)按照分層抽樣的方法,從評定等級為“合格”和“不合格”的問卷中隨機抽取10份進行問題跟蹤調研,現再從這10份問卷中任選4份,記所選4份問卷的量化總分為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() ;
;
(3)某評估機構以指標![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)來評估該市創衛活動的成效.若
的方差)來評估該市創衛活動的成效.若![]() ,則認定創衛活動是有效的;否則認為創衛活動無效,應該調整創衛活動方案.在(2)的條件下,判斷該市是否應該調整創衛活動方案?
,則認定創衛活動是有效的;否則認為創衛活動無效,應該調整創衛活動方案.在(2)的條件下,判斷該市是否應該調整創衛活動方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
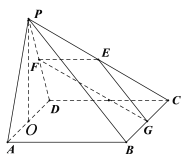
(Ⅰ)求證:PO平面![]() ;
;
(Ⅱ)求平面EFG與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,若存在,求線段
,若存在,求線段![]() 的長度;若不存在,說明理由.
的長度;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有四個函數①y=x|sinx|,②y=xcos|x|,③![]() ,④y=xln|x|的部分圖象如下,但順序被打亂,則按照圖象從左到右的順序,對應的函數序號正確的一組是( )
,④y=xln|x|的部分圖象如下,但順序被打亂,則按照圖象從左到右的順序,對應的函數序號正確的一組是( )
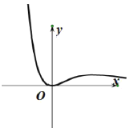
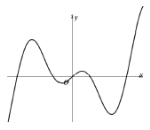
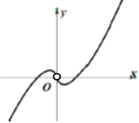
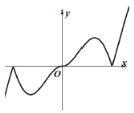
A.①④②③B.①④③②C.③②④①D.③④②①
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年11月份,全國工業生產者出廠價格同比下降![]() ,環比下降
,環比下降![]() 某企業在了解市場動態之后,決定根據市場動態及時作出相應調整,并結合企業自身的情況作出相應的出廠價格,該企業統計了2019年1~10月份產品的生產數量
某企業在了解市場動態之后,決定根據市場動態及時作出相應調整,并結合企業自身的情況作出相應的出廠價格,該企業統計了2019年1~10月份產品的生產數量![]() (單位:萬件)以及銷售總額
(單位:萬件)以及銷售總額![]() (單位:十萬元)之間的關系如下表:
(單位:十萬元)之間的關系如下表:
| 2.08 | 2.12 | 2.19 | 2.28 | 2.36 | 2.48 | 2.59 | 2.68 | 2.80 | 2.87 |
| 4.25 | 4.37 | 4.40 | 4.55 | 4.64 | 4.75 | 4.92 | 5.03 | 5.14 | 5.26 |
(1)計算![]() 的值;
的值;
(2)計算相關系數![]() ,并通過
,并通過![]() 的大小說明
的大小說明![]() 與
與![]() 之間的相關程度;
之間的相關程度;
(3)求![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,并推測當產量為3.2萬件時銷售額為多少.(該問中運算結果保留兩位小數)
,并推測當產量為3.2萬件時銷售額為多少.(該問中運算結果保留兩位小數)
附:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為
中的斜率和截距的最小二乘估計公式分別為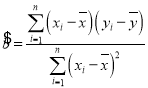 ,
,![]() ;
;
相關系數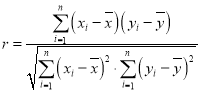 .
.
參考數據: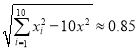 ,
,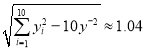 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() ).
).
(Ⅰ)若![]() 是函數
是函數![]() 的一個極值點,求
的一個極值點,求![]() 的值;
的值;
(Ⅱ)求證:當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
(Ⅲ)若對任意的![]() (1,2),總存在
(1,2),總存在![]() ,使不等式
,使不等式![]() 成立,求實數
成立,求實數![]() 的取范圍.
的取范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了提高學生的身體素質,某校高一、高二兩個年級共336名學生同時參與了“我運動,我健康,我快樂”的跳繩、踢毽等系列體育健身活動.為了了解學生的運動狀況,采用分層抽樣的方法從高一、高二兩個年級的學生中分別抽取7名和5名學生進行測試.下表是高二年級的5名學生的測試數據(單位:個/分鐘):

(1)求高一、高二兩個年級各有多少人?
(2)設某學生跳繩![]() 個/分鐘,踢毽
個/分鐘,踢毽![]() 個/分鐘.當
個/分鐘.當![]() ,且
,且![]() 時,稱該學生為“運動達人”.
時,稱該學生為“運動達人”.
①從高二年級的學生中任選一人,試估計該學生為“運動達人”的概率;
②從高二年級抽出的上述5名學生中,隨機抽取3人,求抽取的3名學生中為“運動達人”的人數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com