
【題目】已知函數f(x)=x3﹣ax2+bx+c(a,b,c∈R).
(1)若函數f(x)在x=﹣1和x=3處取得極值,試求a,b的值;
(2)在(1)的條件下,當x∈[﹣2,6]時,f(x)<2|c|恒成立,求c的取值范圍.
【答案】(1)![]() ; (2)(-∞,-18)∪(54,+∞).
; (2)(-∞,-18)∪(54,+∞).
【解析】
(1)根據函數的極值的概念得到方程組解出參數值即可;(2)對函數求導得到函數的單調性和極值,進而得到函數的最大值為c+54,要使f(x)<2|c|恒成立,只要c+54<2|c|即可.
(1)f′(x)=3x2-2ax+b,
∵函數f(x)在x=-1和x=3處取得極值,
∴-1,3是方程3x2-2ax+b=0的兩根.
∴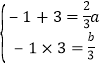 ∴
∴![]() .
.
經檢驗滿足題意.
(2)由(1)知f(x)=x3-3x2-9x+c,
f′(x)=3x2-6x-9.令f′(x)=0,得x=-1或x=3.
當x變化時,f′(x),f(x)隨x的變化情況如下表:
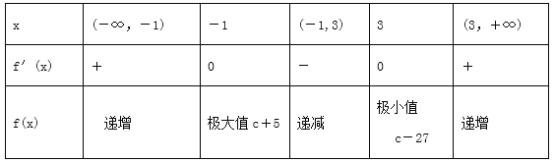
而f(-2)=c-2,f(6)=c+54,
∴當x∈[-2,6]時,f(x)的最大值為c+54,
要使f(x)<2|c|恒成立,只要c+54<2|c|即可,
當c≥0時,c+54<2c,∴c>54 ,
當c<0時,c+54<-2c,∴c<-18.
∴c∈(-∞,-18)∪(54,+∞),此即為實數c的取值范圍.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
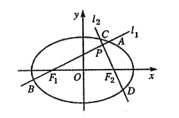
【題目】如圖,分別過橢圓![]() 左、右焦點
左、右焦點![]() 的動直線
的動直線![]() 相交于
相交于![]() 點,與橢圓
點,與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點,直線
不同四點,直線![]() 的斜率
的斜率![]() 滿足
滿足![]() .已知當
.已知當![]() 與
與![]() 軸重合時,
軸重合時,![]() ,
,![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出
為定值?若存在,求出![]() 點坐標并求出此定值;若不存在,說明理由.
點坐標并求出此定值;若不存在,說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】試題分析:(1)當![]() 與
與![]() 軸重合時,
軸重合時,![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,得
,得![]() ,
,![]() 從而得橢圓的方程;(2)由題目分析如果存兩定點,則
從而得橢圓的方程;(2)由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,所以把
點的軌跡是橢圓或者雙曲線 ,所以把![]() 坐標化,可得
坐標化,可得![]() 點的軌跡是橢圓,從而求得定點
點的軌跡是橢圓,從而求得定點![]() 和點
和點![]() .
.
試題解析:![]() 當
當![]() 與
與![]() 軸重合時,
軸重合時,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
![]() 焦點
焦點![]() 坐標分別為
坐標分別為![]() , 當直線
, 當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() ;
;
當直線![]()
![]() 斜率存在時,設斜率分別為
斜率存在時,設斜率分別為![]() , 設
, 設![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 則:
, 則:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因為
, 因為
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由題意知
, 由題意知![]() , 所以
, 所以
![]() , 設
, 設![]() ,則
,則![]() ,即
,即![]() ,由當直線
,由當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() 也滿足此方程,所以點
也滿足此方程,所以點![]() 在橢圓
在橢圓![]() 上.存在點
上.存在點![]() 和點
和點![]() ,使得
,使得![]() 為定值,定值為
為定值,定值為![]() .
.
考點:圓錐曲線的定義,性質,方程.
【方法點晴】本題是對圓錐曲線的綜合應用進行考查,第一問通過兩個特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,從而得橢圓的方程,第二問由題目分析如果存兩定點,則
,從而得橢圓的方程,第二問由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把
點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把![]() 坐標化,求得
坐標化,求得![]() 點的軌跡方程是橢圓
點的軌跡方程是橢圓![]() ,從而求得存在兩定點
,從而求得存在兩定點![]() 和點
和點![]() .
.
【題型】解答題
【結束】
21
【題目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的極值;
的極值;
(Ⅱ)若函數![]() 的兩個零點為
的兩個零點為![]() ,記
,記![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A、B、C的對邊分別是a、b、c,且2sin2A+3cos(B+C)=0.
(1)求角A的大小;
(2)若△ABC的面積S=![]() ,求sinB+sinC的值.
,求sinB+sinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣1+alnx.(e為自然對數的底數),λ=min{a+2,5}.(min{a,b}表示a,b中較小的數.)
(1)當a=0時,設g(x)=f(x)﹣x,求函數g(x)在[![]() ,
,![]() ]上的最值;
]上的最值;
(2)當x![]() 1時,證明:f(x)+x2
1時,證明:f(x)+x2![]() λ(x﹣1)+2.
λ(x﹣1)+2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某漁業公司今年初用98萬元購進一艘遠洋漁船,每年的捕撈可有50萬元的總收入,已知使用![]() 年(
年(![]() )所需(包括維修費)的各種費用總計為
)所需(包括維修費)的各種費用總計為![]() 萬元.
萬元.
(1)該船撈捕第幾年開始贏利(總收入超過總支出,今年為第一年)?
(2)該船若干年后有兩種處理方案:
①當贏利總額達到最大值時,以8萬元價格賣出;
②當年平均贏利達到最大值時,以26萬元賣出,問哪一種方案較為合算?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】挑選空間飛行員可以說是“萬里挑一”,要想通過需要五關:目測、初檢、復檢、文考(文化考試)、政審.若某校甲、乙、丙三位同學都順利通過了前兩關,根據分析甲、乙、丙三位同學通過復檢關的概率分別是0.5、0.6、0.75,能通過文考關的概率分別是0.6、0.5、0.4,由于他們平時表現較好,都能通過政審關,若后三關之間通過與否沒有影響.
(1)求甲被錄取成為空軍飛行員的概率;
(2)求甲、乙、丙三位同學中恰好有一個人通過復檢的概率;
(3)設只要通過后三關就可以被錄取,求錄取人數![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著城市地鐵建設的持續推進,市民的出行也越來越便利.根據大數據統計,某條地鐵線路運行時,發車時間間隔t(單位:分鐘)滿足:![]() ,平均每趟地鐵的載客人數
,平均每趟地鐵的載客人數![]() (單位:人)與發車時間間隔
(單位:人)與發車時間間隔![]() 近似地滿足下列函數關系:
近似地滿足下列函數關系: ,其中
,其中![]() .
.
(1)若平均每趟地鐵的載客人數不超過1000人,試求發車時間間隔t的值;
(2)若平均每趟地鐵每分鐘的凈收益為![]()
![]() (單位:元),問當發車時間間隔t為多少分鐘時,平均每趟地鐵每分鐘的凈收益最大? 并求出最大凈收益.
(單位:元),問當發車時間間隔t為多少分鐘時,平均每趟地鐵每分鐘的凈收益最大? 并求出最大凈收益.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com