
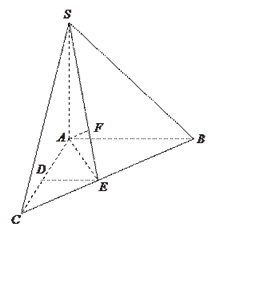
【題目】如圖,在三棱錐![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,
的中點, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)在線段上![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角
![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)見解析; (2)見解析.
【解析】試題分析:第(1)問證明![]() 平面
平面![]() ,基本思路是證明
,基本思路是證明![]() 平面
平面![]() 內的兩條相交直線垂直,注意合理利用題設條件給出的數量關系和圖形關系;第(2)問應抓住兩點找到問題的求解方向:一是點
內的兩條相交直線垂直,注意合理利用題設條件給出的數量關系和圖形關系;第(2)問應抓住兩點找到問題的求解方向:一是點![]() 的預設位置,二是二面角
的預設位置,二是二面角![]() 的位置.涉及空間二面角的問題,可以從兩個不同的方法上得到求解,即常規法和向量法
的位置.涉及空間二面角的問題,可以從兩個不同的方法上得到求解,即常規法和向量法
試題解析:
(1)由![]() ,
, ![]() ,
,
![]() 是
是![]() 的中點,得
的中點,得![]() .
.
因為![]() 底面
底面![]() ,所以
,所以![]() .
.
 在
在![]() 中,
中, ![]() ,所以
,所以![]() .
.
因此![]() ,又因為
,又因為![]() ,
,
所以![]() ,
,
則![]() ,即
,即![]() . 因為
. 因為![]() 底面
底面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 底面
底面![]() ,則
,則![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)方法一:假設滿足條件的點![]() 存在,并設
存在,并設![]() .
.
過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,
,
又由![]() ,
, ![]() ,得
,得![]() 平
平
面![]() .
.
作![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() ,則
,則![]() .
.
于是![]() 為二面角
為二面角![]() 的平面角,
的平面角,
即![]() ,由此可得
,由此可得![]() .
.
由![]() ,得
,得![]() ,于是有
,于是有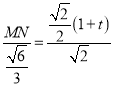 ,
, ![]() .
.
在![]() 中,
中, ![]() ,即
,即![]() ,解得
,解得![]() .
.
于是滿足條件的點![]() 存在,且
存在,且![]() .
.
(2)方法二:假設滿足條件的點![]() 存在,并設
存在,并設![]() .以
.以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
, ![]() ,
, ![]() 為
為![]() ,
, ![]() ,
, ![]() 軸建立空間直線坐標系
軸建立空間直線坐標系
![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
,
![]() .由
.由![]() 得
得![]() .
.
所以![]() ,
, ![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則
 ,即
,即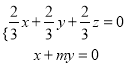 ,取
,取![]() ,得
,得![]() ,
, ![]() ,即
,即![]() .設平面
.設平面![]() 的法向量為
的法向量為![]() ,則
,則 ,即
,即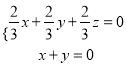 ,取
,取![]() ,得
,得![]() ,
, ![]() ,即
,即![]() .由二面角
.由二面角![]() 的大小為
的大小為![]() ,得
,得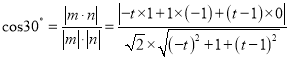 ,化簡得
,化簡得![]() ,又
,又![]() ,求得
,求得![]() . 于是滿足條件的點
. 于是滿足條件的點![]() 存在,且
存在,且![]() .
.
點晴:本題考查的是線面垂直的明和二面角的求解.第(1)問證明![]() 平面
平面![]() ,基本思路是證明
,基本思路是證明![]() 平面
平面![]() 內的兩條相交直線垂直,注意合理利用題設條件給出的數量關系和圖形關系;第(2)問應抓住兩點找到問題的求解方向:一是點
內的兩條相交直線垂直,注意合理利用題設條件給出的數量關系和圖形關系;第(2)問應抓住兩點找到問題的求解方向:一是點![]() 的預設位置,二是二面角
的預設位置,二是二面角![]() 的位置.涉及空間二面角的問題,可以從兩個不同的方法上得到求解,即常規法和向量法
的位置.涉及空間二面角的問題,可以從兩個不同的方法上得到求解,即常規法和向量法


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面A1B1C1 , 底面為直角三角形,∠ACB=90°,AC=2,BC=1,CC1= ![]() ,P是BC1上一動點,則A1P+PC的最小值是 .
,P是BC1上一動點,則A1P+PC的最小值是 . 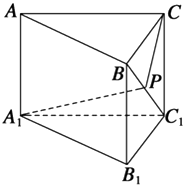
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:若實數x滿足x2﹣4ax+3a2≤0,其中a>0;命題q:實數x滿足 ![]()
(1)若a=1且p∧q為真,求實數x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Sn是等差數列{an}的前n項和,且S6>S7>S5 , 給出下列五個命題:①d<1;②S11>0;③S12<0;④數列{Sn}中的最大項為S11;⑤|a6|>|a7|.其中正確命題有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C所對的邊分別為a,b,c.向量 ![]() =(a,
=(a, ![]() b)與
b)與 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面積.
,b=2,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1的棱長為1,線段B1D1上有兩個動點E,F,且EF= ![]() ,給出下列結論:
,給出下列結論:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱錐A﹣BEF的體積為定值;
(4)異面直線AE,BF所成的角為定值.
其中錯誤的結論有( )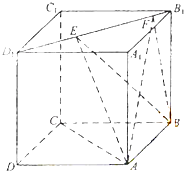
A.0個
B.1 個
C.2個
D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=3,an+1﹣3an=3n(n∈N*),數列{bn}滿足bn= ![]() .
.
(Ⅰ)求證:數列{bn}是等差數列,并求數列{an}的通項公式;
(Ⅱ)求數列{an}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com