
【題目】已知橢圓C: ![]() 的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D
的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D ![]() 在橢圓C上,直線l:y=kx+m與橢圓C相交于A、P兩點,與x軸、y軸分別相交于點N和M,且PM=MN,點Q是點P關于x軸的對稱點,QM的延長線交橢圓于點B,過點A、B分別作x軸的垂涎,垂足分別為A1、B1
在橢圓C上,直線l:y=kx+m與橢圓C相交于A、P兩點,與x軸、y軸分別相交于點N和M,且PM=MN,點Q是點P關于x軸的對稱點,QM的延長線交橢圓于點B,過點A、B分別作x軸的垂涎,垂足分別為A1、B1
(1)求橢圓C的方程;
(2)是否存在直線l,使得點N平分線段A1B1?若存在,求求出直線l的方程,若不存在,請說明理由.
【答案】
(1)
解:∵橢圓C: ![]() 的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D
的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D ![]() 在橢圓C上,
在橢圓C上,
∴由題意得 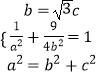 ,解得a2=4,b2=3,
,解得a2=4,b2=3,
∴橢圓C的方程為 ![]() .
.
(2)
解:假設存在這樣的直線l:y=kx+m,∴M(0,m),N(﹣ ![]() ,0),
,0),
∵PM=MN,∴P( ![]() ,2m),Q(
,2m),Q( ![]() ),
),
∴直線QM的方程為y=﹣3kx+m,
設A(x1,y1),由 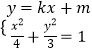 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
∴ ![]() ,∴
,∴ ![]() ,
,
設B(x2,y2),由 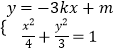 ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
∴x2+ ![]() =
= ![]() ,∴x2=﹣
,∴x2=﹣ ![]() ,
,
∵點N平分線段A1B1,∴ ![]() ,
,
∴﹣ ![]() =﹣
=﹣ ![]() ,∴k=
,∴k= ![]() ,
,
∴P(±2m,2m),∴ ![]() ,解得m=
,解得m= ![]() ,
,
∵|m|= ![]() <b=
<b= ![]() ,∴△>0,符合題意,
,∴△>0,符合題意,
∴直線l的方程為y= ![]()
【解析】(1)由橢圓的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D ![]() 在橢圓C上,列出方程組,求出a,b,由此能求出橢圓C的方程.(2)假設存在這樣的直線l:y=kx+m,則直線QM的方程為y=﹣3kx+m,由
在橢圓C上,列出方程組,求出a,b,由此能求出橢圓C的方程.(2)假設存在這樣的直線l:y=kx+m,則直線QM的方程為y=﹣3kx+m,由 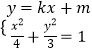 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由 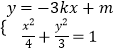 ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判別式、韋達定理、中點坐標公式,結合已知條件,能求出直線l的方程.
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判別式、韋達定理、中點坐標公式,結合已知條件,能求出直線l的方程.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2.5cos(ωx+φ)(ω>0,|φ|< ![]() )的部分圖象如圖所示,M、N兩點之間的距離為13,且f(3)=0,若將函數f(x)的圖象向右平移t(t>0)個單位長度后所得函數的圖象關于坐標原點對稱,則t的最小值為( )
)的部分圖象如圖所示,M、N兩點之間的距離為13,且f(3)=0,若將函數f(x)的圖象向右平移t(t>0)個單位長度后所得函數的圖象關于坐標原點對稱,則t的最小值為( ) 
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省GDP情況圖,則下列陳述中不正確的是( )
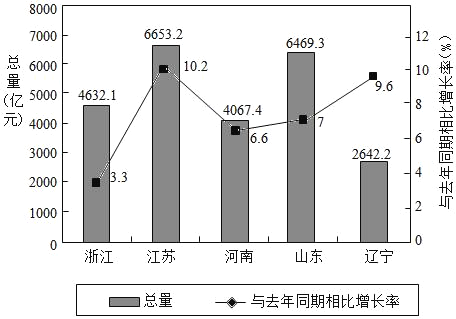
A. 2017年第一季度![]() 總量和增速由高到低排位均居同一位的省只有1個
總量和增速由高到低排位均居同一位的省只有1個
B. 與去年同期相比,2017年第一季度五個省的![]() 總量均實現了增長
總量均實現了增長
C. 去年同期河南省的![]() 總量不超過4000億元
總量不超過4000億元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為D的函數y=f(x),如果存在區間[m,n]D,其中m<n,同時滿足:①f(x)在[m,n]內是單調函數;②當定義域是[m,n]時,f(x)的值域也是[m,n]. 則稱函數f(x)是區間[m,n]上的“保值函數”,區間[m,n]稱為“保值區間”.
(1)求證:函數g(x)=x2﹣2x不是定義域[0,1]上的“保值函數”.
(2)若函數f(x)=2+ ![]() ﹣
﹣ ![]() (a∈R,a≠0)是區間[m,n]上的“保值函數”,求a的取值范圍.
(a∈R,a≠0)是區間[m,n]上的“保值函數”,求a的取值范圍.
(3)對(2)中函數f(x),若不等式|a2f(x)|≤2x對x≥1恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]()
(1)若不等式f(x)﹣f(x+m)≤1恒成立,求實數m的最大值;
(2)當a< ![]() 時,函數g(x)=f(x)+|2x﹣1|有零點,求實數a的取值范圍.
時,函數g(x)=f(x)+|2x﹣1|有零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,直線
,直線![]() .
.
(1)求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;
垂直的直線方程;
(2)在直線![]() 上(
上(![]() 為坐標原點),存在定點
為坐標原點),存在定點![]() (不同于點
(不同于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:
(1)設所求直線方程為![]() ,利用圓心到直線的距離等于半徑可得關于b的方程,解方程可得
,利用圓心到直線的距離等于半徑可得關于b的方程,解方程可得![]() ,則所求直線方程為
,則所求直線方程為![]()
(2)方法1:假設存在這樣的點![]() ,由題意可得
,由題意可得![]() ,則
,則![]() ,然后證明
,然后證明![]() 為常數
為常數![]() 為即可.
為即可.
方法2:假設存在這樣的點![]() ,使得
,使得![]() 為常數
為常數![]() ,則
,則![]() ,據此得到關于
,據此得到關于![]() 的方程組,求解方程組可得存在點
的方程組,求解方程組可得存在點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為常數
為常數![]() .
.
試題解析:
(1)設所求直線方程為![]() ,即
,即![]() ,
,
∵直線與圓相切,∴![]() ,得
,得![]() ,
,
∴所求直線方程為![]()
(2)方法1:假設存在這樣的點![]() ,
,
當![]() 為圓
為圓![]() 與
與![]() 軸左交點
軸左交點![]() 時,
時,![]() ;
;
當![]() 為圓
為圓![]() 與
與![]() 軸右交點
軸右交點![]() 時,
時,![]() ,
,
依題意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() .
.
下面證明點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數.
為一常數.
設![]() ,則
,則![]() ,
,
∴![]()
![]()
![]() ,
,
從而![]() 為常數.
為常數.
方法2:假設存在這樣的點![]() ,使得
,使得![]() 為常數
為常數![]() ,則
,則![]() ,
,
∴![]() ,將
,將![]() 代入得,
代入得,
![]() ,即
,即
![]() 對
對![]() 恒成立,
恒成立,
∴![]() ,解得
,解得 或
或![]() (舍去),
(舍去),
所以存在點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為常數
為常數![]() .
.
點睛:求定值問題常見的方法有兩種:
(1)從特殊入手,求出定值,再證明這個值與變量無關.
(2)直接推理、計算,并在計算推理的過程中消去變量,從而得到定值.
【題型】解答題
【結束】
22
【題目】已知函數![]() 的導函數為
的導函數為![]() ,其中
,其中![]() 為常數.
為常數.
(1)當![]() 時,求
時,求![]() 的最大值,并推斷方程
的最大值,并推斷方程![]() 是否有實數解;
是否有實數解;
(2)若![]() 在區間
在區間![]() 上的最大值為-3,求
上的最大值為-3,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某機械廠要將長![]() ,寬
,寬![]() 的長方形鐵皮
的長方形鐵皮![]() 進行裁剪.已知點
進行裁剪.已知點![]() 為
為![]() 的中點,點
的中點,點![]() 在邊
在邊![]() 上,裁剪時先將四邊形
上,裁剪時先將四邊形![]() 沿直線
沿直線![]() 翻折到
翻折到![]() 處(點
處(點![]() 分別落在直線
分別落在直線![]() 下方點
下方點![]() 處,
處,![]() 交邊
交邊![]() 于點
于點![]() ),再沿直線
),再沿直線![]() 裁剪.
裁剪.

(1)當![]() 時,試判斷四邊形
時,試判斷四邊形![]() 的形狀,并求其面積;
的形狀,并求其面積;
(2)若使裁剪得到的四邊形![]() 面積最大,請給出裁剪方案,并說明理由.
面積最大,請給出裁剪方案,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com