【題目】已知圓
：
，直線
被圓所截得的弦的中點為P（5，3）．（1）求直線的方程；（2）若直線
：
與圓相交于兩個不同的點，求b的取值范圍.
【答案】（1）
（2）
【解析】
（I）根據圓心CP與半徑垂直，可求出直線l1的斜率，進而得到點斜式方程，再化成一般式即可.
（II）根據直線與圓的位置關系，圓心到直線的距離小于半徑得到關于b的不等式，從而解出b的取值范圍.
（1）由
，得
，
∴圓心
，半徑為3.…………………2分
由垂徑定理知直線
直線
，
直線的斜率
，故直線
的斜率
，……………5分
∴直線的方程為
，即.…………………7分
（2）解法1：由題意知方程組
有兩組解，由方程組消去
得
，該方程應有兩個不同的解，…………………9分
∴
，化簡得
，………………10分
由
解得
∴的解為.…………………………13分
故b的取值范圍是.…………………………14分
解法2：同（1）有圓心，半徑為3.…………………9分
由題意知，圓心到直線
：
的距離小于圓的半徑，即
，即
，………………………11分
解得
，………………………13分
故b的取值范圍是.…………………14分
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}是無窮數列，滿足lgan+1=|lgan﹣lgan﹣1|（n=2，3，4，…）．
（1）若a1=2，a2=3，求a3 ， a4 ， a5的值；
（2）求證：“數列{an}中存在ak（k∈N*）使得lgak=0”是“數列{an}中有無數多項是1”的充要條件；
（3）求證：在數列{an}中ak（k∈N*），使得1≤ak＜2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A（﹣
，0）和B（，0），動點C到A、B兩點的距離之差的絕對值為2．
（1）求點C的軌跡方程；
（2）點C的軌跡與經過點（2，0）且斜率為1的直線交于D、E兩點，求線段DE的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sin2ωx（ω＞0），將y=f（x）的圖象向右平移 
個單位長度后，若所得圖象與原圖象重合，則ω的最小值等于（ ）
A.2
B.4
C.6
D.8
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】第 
屆夏季奧林匹克運動會將于2016年8月5日 
21日在巴西里約熱內盧舉行．下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據（單位：枚）．
| 第31屆里約 | 第30屆倫敦 | 第29屆北京 | 第28屆雅典 | 第27屆悉尼 |
中國 | 26 | 38 | 51 | 32 | 28 |
俄羅斯 | 19 | 24 | 24 | 27 | 32 |
（1）根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖，并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度（不要求計算出具體數值，給出結論即可）；
（2）下表是近五屆奧運會中國代表團獲得的金牌數之和 
（從第 
屆算起，不包括之前已獲得的金牌數）隨時間 
（時間代號）變化的數據：
屆 | 27 | 28 | 29 | 30 | 31 |
時間代號(x) | 1 | 2 | 3 | 4 | 5 |
金牌數之和(y枚) | 28 | 60 | 111 | 149 | 175 |
作出散點圖如下：
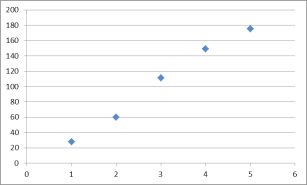
①由圖中可以看出，金牌數之和 與時間代號 之間存在線性相關關系，請求出 關于 的線性回歸方程；
②利用①中的回歸方程，預測2020年第32屆奧林匹克運動會中國代表團獲得的金牌數．
參考數據：
，
，
．
附：對于一組數據 
，
，
，
，其回歸直線
的斜率的最小二乘估計為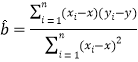
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】第 
屆夏季奧林匹克運動會將于2016年8月5日 
21日在巴西里約熱內盧舉行．下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據（單位：枚）．
| 第31屆里約 | 第30屆倫敦 | 第29屆北京 | 第28屆雅典 | 第27屆悉尼 |
中國 | 26 | 38 | 51 | 32 | 28 |
俄羅斯 | 19 | 24 | 24 | 27 | 32 |
（1）根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖，并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度（不要求計算出具體數值，給出結論即可）；
（2）下表是近五屆奧運會中國代表團獲得的金牌數之和 
（從第 
屆算起，不包括之前已獲得的金牌數）隨時間 
（時間代號）變化的數據：
屆 | 27 | 28 | 29 | 30 | 31 |
時間代號(x) | 1 | 2 | 3 | 5 | |
金牌數之和(y枚) | 28 | 60 | 111 | 149 | 175 |
作出散點圖如下：
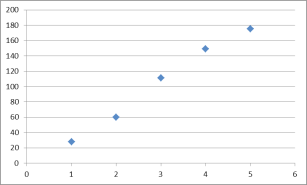
①由圖中可以看出，金牌數之和 與時間代號 之間存在線性相關關系，請求出 關于 的線性回歸方程；
②利用①中的回歸方程，預測2020年第32屆奧林匹克運動會中國代表團獲得的金牌數．
參考數據：
，
，
．
附：對于一組數據 
，
，
，
，其回歸直線
的斜率的最小二乘估計為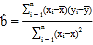
．
查看答案和解析>>
科目：高中數學 來源： 題型：
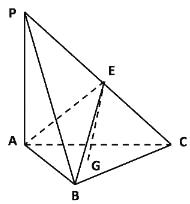
【題目】如圖，在三棱錐P﹣ABC中，平面PAC⊥平面ABC，PA⊥AC，AB=BC=CA=AP=2，G是△ABC重心，E是線段PC上一點，且CE=λCP．
（1）當EG∥平面PAB時，求λ的值；
（2）當直線CP與平面ABE所成角的正弦值為
時，求λ的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P﹣ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC與BD的交點M恰好是AC中點，又PA=4，AB=4 
，∠CDA=120°，點N在線段PB上，且PN=2． 
（1）求證：BD⊥PC；
（2）求證：MN∥平面PDC；
（3）求二面角A﹣PC﹣B的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
